Bài 59 trang 90 SGK Toán 9 tập 2

Giải SGK Toán 9

1 Đánh giá

Toán 9 Bài 7 Tứ giác nội tiếp

Giải Toán 9 Bài 59 Trang 90 SGK Tứ giác nội tiếp với hướng dẫn và lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa môn Toán 9, các bài giải tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải Toán 9.

Bài 59 trang 90 SGK Toán 9 tập 2

Bài 59 (SGK trang 90): Cho hình bình hành ABCD. Đường tròn đi qua ba đỉnh A, B, C cắt đường thẳng CD tại P khác C. Chứng minh AP = AD.

Hướng dẫn giải

Trong một tứ giác nội tiếp, tổng số đo góc hai góc đối nhau bằng 180⁰

Lời giải chi tiết

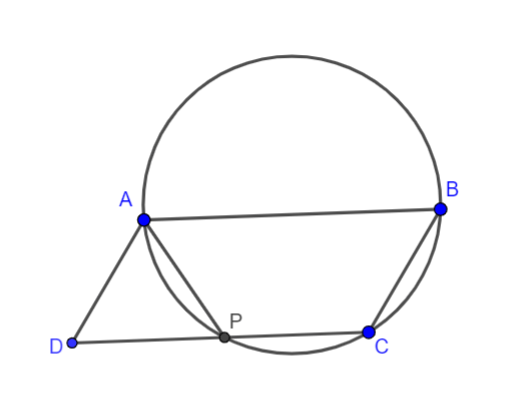
Bài 59 trang 90 SGK Toán 9 tập 2

Ta có: AB // CD (Do ABCD là hình bình hành) $\Rightarrow \widehat {ABC} + \widehat {BCP} = {180^0}$ (tính chất) (*)

Ta lại có ABCP là tứ giác nội tiếp $\Rightarrow \widehat {BAP} + \widehat {BCP} = {180^0}$ (**)

Từ (*) và (**) $\Rightarrow \widehat {BAP} = \widehat {ABC}$

Ta có: PC // AB nên ABCP là hình thang

Do $\widehat {BAP} = \widehat {ABC}$ nên ABCP là hình thang cân $\Rightarrow AP = BC$ (1)

Mà ABCD là hình bình hành $\Rightarrow AD = BC$ (2)

Từ (1) và (2) $\Rightarrow AD = AP$

------------------------------------------------

Trên đây GiaiToan đã chia sẻ Giải Toán 9: Tứ giác nội tiếp. Hy vọng với tài liệu này sẽ giúp ích cho các bạn học sinh tham khảo, chuẩn bị cho bài giảng sắp tới tốt hơn. Chúc các bạn học tập tốt!