Bài 4.20 trang 79 Toán 7 tập 1 SGK Kết nối tri thức với cuộc sống Giải Toán 7 Kết nối tri thức
Bài 4.20 trang 79 SGK Toán 7
Toán 7 Bài 4.20 trang 79 Các trường hợp bằng nhau của tam giác vuông là lời giải bài SGK Toán 7 Tập 1 KNTT hướng dẫn chi tiết lời giải giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải Toán 7. Mời các em học sinh cùng tham khảo chi tiết.
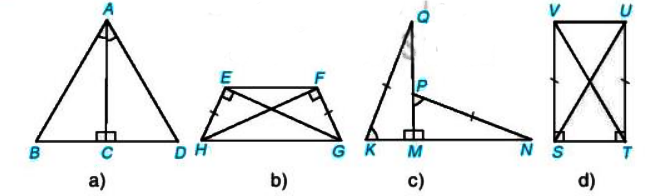
Bài 4.20 (SGK trang 79): Mỗi hình sau có các cặp tam giác vuông nào bằng nhau? Vì sao?
|
Hướng dẫn giải
Các trường hợp bằng nhau của tam giác vuông:
Trường hợp 1: Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Trường hợp 2: Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Trường hợp 3: Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Lời giải chi tiết
a) Hình a:
Xét tam giác ABC vuông tạo C và tam giác ADC vuông tạo C ta có:
AC là cạnh chung
![]() (giả thiết)
(giả thiết)
Do đó ∆ ABC = ∆ ADC (g - c - g)
Vậy hình a có cặp tam giác vuông ABC và ADC bằng nhau.
b)Hình b:
Xét tam giác EHG vuông tạo E và tam giác HFG vuông tạo F ta có:
EH = FG
HG là cạnh chung
Do đó ∆ EHG = ∆ HFG (cạnh huyền - cạnh góc vuông)
Vậy hình b có cặp tam giác vuông EHG và HFG bằng nhau.
c) Hình c:
Xét tam giác KMQ vuông tạo M và tam giác PMN vuông tạo M ta có:
KQ = PN
![]() (giả thiết)
(giả thiết)
Do đó ∆ KMQ = ∆ PMN (cạnh huyền - góc nhọn)
Vậy hình c có cặp tam giác vuông KMQ và PMN bằng nhau.
d) Hình d:
Xét tam giác VST vuông tạo S và tam giác UTS vuông tạo T ta có:
VS = UT
ST là cạnh chung
Do đó ∆ VST = ∆ UTS (c - g - c)
Xét tam giác VUS vuông tạo V và tam giác VUT vuông tạo U ta có:
VS = UT
VU là cạnh chung
Do đó ∆ VUS = ∆ VUT (c - g - c)
Vậy hình d có 2 cặp tam giác vuông bằng nhau là ∆VUS, ∆VUT và cặp ∆VST, ∆UTS
-----> Câu hỏi cùng bài:
- Luyện tập 3 (SGK trang 79): Cho ba điểm A, B, C nằm trên đường tròn tâm O ...
- Thử thách nhỏ (SGK trang 79): Có hai chiếc thang dài như nhau được ...
- Bài 4.21 (SGK trang 79): Cho hình 4.56, biết AB = CD,
 ...
... - Bài 4.22 (SGK trang 79): Cho hình chữ nhật ABCD, M là trung điểm của cạnh BC ...
------> Bài liên quan: Giải Toán 7 Bài 15 Các trường hợp bằng nhau của tam giác vuông
----------------------------------------
Trên đây là lời giải chi tiết Bài 4.20 Toán 7 trang 79 Các trường hợp bằng nhau của tam giác vuông cho các em học sinh tham khảo, nắm được cách giải các dạng toán của Chương 4: Tam giác bằng nhau. Qua đó giúp các em học sinh ôn tập chuẩn bị cho các bài thi giữa và cuối học kì lớp 7. Chúc các em học tốt.
Ngoài ra Giaitoan mời thầy cô và học sinh tham khảo thêm một số tài liệu liên quan: Luyện tập Toán 7, Đề thi giữa học kì 1 Toán 7, Đề thi học kì 1 Toán 7, ....
- Lượt xem: 9.963