Bài 10 trang 63 SGK Toán 8 tập 2

Giải SGK Toán 8

1 Đánh giá

Toán 8 Bài 2: Định lý đảo và hệ quả của định lí Ta - lét

Bài 10 Trang 63 SGK Toán 8 tập 2 biên soạn và đăng tải với hướng dẫn chi tiết lời giải giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải Toán 8. Mời các em học sinh cùng tham khảo chi tiết.

Bài 10 Trang 63 SGK Toán 8 - Tập 2

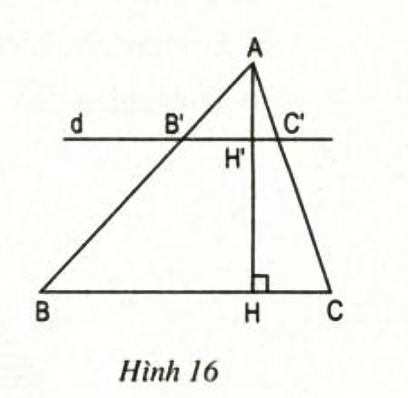
Bài 10 (SGK trang 63): Cho tam giác ABC có đường cao AH. Đường thẳng d song song với BC, cắt các cạnh AB, AC và đường cao AH theo thứ tự tại các điểm B’, C’ và H’ (h.16)

a. Chứng minh rằng: $\frac{AH'}{AH}=\frac{B'C'}{BC}$

b. Áp dụng: Cho biết $AH'=\frac{1}{3}AH$ và diện tích tam giác ABC là $67,5c{{m}^{2}}$ . Tính diện tích tam giác AB’C’.

Bài 10 Trang 63 SGK Toán 8 tập 2

Hướng dẫn giải

- Định lý Talet: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.

- Diện tích tam giác bằn nửa tích chiều cao với cạnh đáy.

Lời giải chi tiết

a) Vì $B^{\prime} C^{\prime} / / B C$ (giả thiết) $\Rightarrow \frac{A H^{\prime}}{A H}=\frac{B^{\prime} H^{\prime}}{B H}=\frac{H^{\prime} C^{\prime}}{H C}$ (hệ quả định lí Ta-lét)

Áp dụng tính chất dãy tỉ số bằng nhau, ta được:

$\frac{A H^{\prime}}{A H}=\frac{B^{\prime} H^{\prime}}{B H}=\frac{H^{\prime} C^{\prime}}{H C}=\frac{B^{\prime} H^{\prime}+H^{\prime} C^{\prime}}{B H+H C}=\frac{B^{\prime} C^{\prime}}{B C}$

Vậy $\frac{A H^{\prime}}{A H}=\frac{B^{\prime} C^{\prime}}{B C}$

b) Ta có: $A H^{\prime}=\frac{1}{3} A H$ (giả thiết) $\Rightarrow \frac{A H^{\prime}}{A H}=\frac{1}{3}$

Lại có: $\frac{A H^{\prime}}{A H}=\frac{B^{\prime} C^{\prime}}{B C}$ (chứng minh trên)

$\Rightarrow \frac{B^{\prime} C^{\prime}}{B C}=\frac{1}{3}$

Gọi S và S' lần lượt là diện tích của tam giác ABC và A’B’C’ ta có $\frac{S^{\prime}}{S}=\dfrac{\dfrac{1}{2} A H^{\prime} \cdot B^{\prime} C^{\prime}}{\dfrac{1}{2} A H . B C}=\dfrac{A H^{\prime}}{A H} \cdot \frac{B^{\prime} C^{\prime}}{B C}=\frac{1}{3} \cdot \frac{1}{3}=\frac{1}{9}$

$\Rightarrow S^{\prime}=\frac{1}{9} \cdot S=\frac{1}{9} \cdot 67,5=7,5\left(\mathrm{~cm}^{2}\right)$

Vây diện tích tam giác A’B’C’ là $7,5 c m^{2}$

_{-------------------------------------------------------------}

Trên đây là lời giải chi tiết bài tập Toán 8 bài 2: Định lý Talet đảo và hệ quả của định lí Talet cho các em học sinh tham khảo, nắm được cách giải các dạng toán Chương 3: Tam giác đồng dạng Toán 8 Tập 2. Với lời giải hướng dẫn chi tiết các bạn có thể so sánh kết quả của mình từ đó nắm chắc kiến thức Toán lớp 8. Chúc các bạn học tốt và nhớ thường xuyên tương tác với GiaiToan để có thêm nhiều tài liệu chất lượng miễn phí nhé!