Giaitoan.com Toán 12 Toán 12 Kết nối tri thức

Luyện tập 5 trang 12 Toán 12 tập 1 Kết nối tri thức Giải Toán 12 Kết nối tri thức Bài 1

Nội dung
  • 1 Đánh giá

Luyện tập 5 trang 12 SGK Toán 12

Toán 12 Luyện tập 5 trang 12 Bài 1 Tính đơn điệu và cực trị của hàm số là lời giải bài SGK Toán 12 sách Kết nối tri thức với cuộc sống hướng dẫn chi tiết lời giải giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải Toán 12 KNTT. Mời các em học sinh cùng tham khảo chi tiết.

Giải Luyện tập 5 Toán 12 trang 12

Luyện tập 5 trang 12 toán 12 tập 1: Tìm cực trị của các hàm số sau:

a) y = x4 - 3x2 + 1

b) y=\frac{-x^2+2x-1}{x+2}

Lời giải chi tiết:

a) y = x4 - 3x2 + 1

Tập xác định của hàm số là R.

Ta có: y' = 4x3 - 6x = 2x(2x2 - 3)

y' = 0 \Leftrightarrow x = 0 hoặc x= -\frac{\sqrt{6} }{2} hoặc x= \frac{\sqrt{6} }{2}

Lập bảng biến thiên của hàm số:

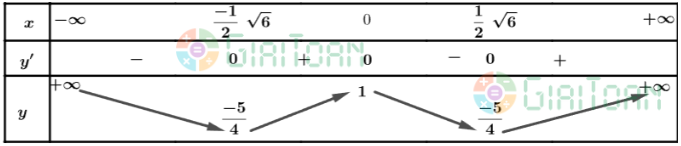
Từ bảng biến thiên, ta có:

Hàm số đạt cực tiểu tại x= -\frac{\sqrt{6} }{2} và yCT = y\left(-\frac{\sqrt{6}}{2}\right)=-\frac{5}{4}

Hàm số đạt cực tiểu tại x= \frac{\sqrt{6} }{2} và yCT = y\left(\frac{\sqrt{6}}{2}\right)=-\frac{5}{4}

Hàm số đạt cực đại tại x = 0 và yCĐ = y(0) = 1.

b) y=\frac{-x^2+2x-1}{x+2}

Tập xác định của hàm số là R \ {- 2}

Ta có: y'=\frac{\left(-2x+2\right)\left(x+2\right)-\left(-x^2+2x-1\right)}{\left(x+2\right)^2}=\frac{-x^2-4x+5}{\left(x+2\right)^2}

y' = 0 \Leftrightarrow x = 1 hoặc x = - 5.

Lập bảng biến thiên của hàm số:

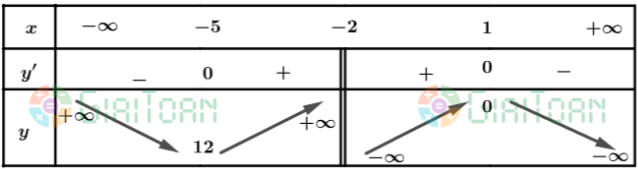
Từ bảng biến thiên, ta có:

Hàm số đạt cực tiểu tại x = - 5 và yCT = y(- 5) = 12

Hàm số đạt cực đại tại x = 1 và yCĐ = y(1) = 0.

---> Câu hỏi cùng bài:

-------> Bài tiếp theo: Giải Toán 12 Bài 2: Giá trị lớn nhất và nhỏ nhất của hàm số

Chia sẻ bởi: Cự Giải
Mời bạn đánh giá!
  • Lượt xem: 439
Tìm thêm: Toán 12 Toán 12 Kết nối tri thức
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần