Giaitoan.com Toán 7 Giải Toán 7 tập 2 KNTT

Luyện tập 1 trang 79 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống Giải Toán 7 sách Kết nối tri thức

Nội dung
  • 8 Đánh giá

Luyện tập 1 trang 79 SGK Toán 7 tập 2

Toán 7 tập 2 Luyện tập 1 trang 79 là lời giải bài Sự đồng quy của ba đường trung trực, ba đường cao SGK Toán 7 sách Kết nối tri thức với cuộc sống hướng dẫn chi tiết lời giải giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải Toán 7. Mời các em học sinh cùng tham khảo chi tiết.

Giải Luyện tập 1 Toán 7 trang 79

Luyện tập 1 (SGK trang 79): Chứng minh rằng trong tam giác đều ABC, trọng tâm G cách đều ba đỉnh của tam giác đó.

Hướng dẫn giải

– Ba đường trung trực của một tam giác đồng quy tại một điểm. Điểm này cách đều ba đỉnh của tam giác.

– Ba đường cao của một tam giác đồng quy tại một điểm. Điểm đồng quy của ba đường cao gọi là trực tâm của tam giác đó.

Lời giải chi tiết

Hình vẽ minh họa:

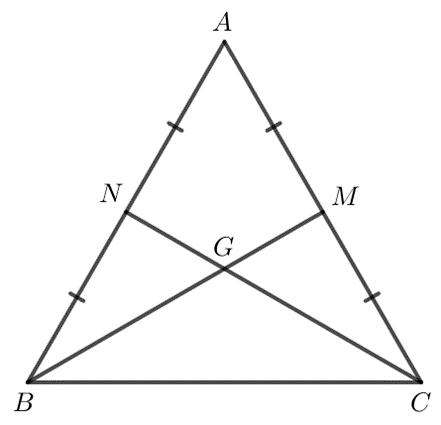
Luyện tập 1 trang 79 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống

Gọi M là giao điểm của BG và AC, N là giao điểm của CG và AB.

Do ∆ ABC đều nên AB = BC = CA và \widehat {ABC} = \widehat {ACB} = \widehat {BAC}

M là trung điểm của AC ⇒ AM = MC

Xét ∆ ABM và ∆ CBM có:

AB = CB (chứng minh trên)

\widehat {BAM} = \widehat {BCM} (chứng minh trên)

AM = CM (chứng minh trên)

⇒ ∆ ABM = ∆ CBM (c – g – c)

⇒\widehat {BAM} = \widehat {BMC} (Hai góc tương ứng)

Mà \widehat {BAM} + \widehat {BMC} = {180^0} \Rightarrow \widehat {BAM} = \widehat {BMC} = {90^0}

⇒ BM ⊥ AC

Ta có: BM ⊥ AC tại trung điểm M của AC nên BM là đường trung trực của AC.

N là trung điểm của AB nên AN = BN.

Xét ∆ CAN và ∆ CBN có:

CA = CB (chứng minh trên)

\widehat {CAN} = \widehat {CBN} (chứng minh trên)

AN = BN (chứng minh trên)

⇒ ∆ CAN = ∆ CBN (c – g – c)

⇒ \widehat {CNA} = \widehat {CNB} (Hai góc tương ứng)

Mà \widehat {CNA} + \widehat {CNB} = {180^0} \Rightarrow \widehat {CNA} = \widehat {CNB} = {90^0}

⇒ CN ⊥ AB

Ta có CN ⊥ AB tại trung điểm N của AB nên CN là đường trung trực của AB.

G là giao điểm 2 đường trung trực của ∆ ABC nên G cách đều 3 đỉnh của tam giác.

→ Câu hỏi cùng bài:

→ Bài liên quan: Giải Toán 7 Kết nối tri thức Bài 35 Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác

→ Bài tiếp theo: Giải Toán 7 Kết nối tri thức Luyện tập chung trang 82

------------------------------------------------

Chia sẻ bởi: Đen2017
Mời bạn đánh giá!
  • Lượt xem: 6.653
Tìm thêm: Toán 7 Giải Toán 7
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần