Giaitoan.com Toán 9 Đề thi học kì 1 lớp 9

Đề thi học kì 1 Toán 9 năm học 2022 – 2023 - Đề số 8 Đề thi cuối kì 1 lớp 9

Nội dung
  • 1 Đánh giá

Đề thi học kì 1 Toán 9 - Đề số 8

Đề thi học kì 1 Toán 9 năm học 2022 – 2023 - Đề số 8 được giaitoan.com biên soạn bao gồm các dạng bài tập và đáp án chi tiết được xây dựng theo trọng tâm chương trình học môn Toán lớp 9 giúp học sinh ôn tập, củng cố kiến thức, giúp định vị khả năng tư duy logic, khả năng nhận biết. Đề thi giúp các em tiếp xúc với các dạng bài cơ bản đến nâng cao thường xuất hiện trong ma trận đề thi HK1 lớp 9, hỗ trợ việc ôn lại nội dung và kiểm soát tốt thời gian làm bài thi. Mời các bạn cùng tham khảo chi tiết.

A. Đề thi Toán kì 1 lớp 9

Câu 1

1) Rút gọn biểu thức sau:

a) \sqrt {20} - \sqrt {80} + 2\sqrt {45}b) \dfrac{1}{{3 - \sqrt 7 }} - \dfrac{1}{{3 + \sqrt 7 }}

2) Giải phương trình sau: \sqrt {25x + 25} - \sqrt {9x + 9} + \sqrt {4x + 4} = 16

3) Giải hệ phương trình sau: \left\{ \begin{array}{l} x + y = 3\\ 4x - y = 2 \end{array} \right.

Câu 2

Cho hai biểu thức A = \dfrac{{4\sqrt x }}{{\,\sqrt x - 2}}  và B = \dfrac{2}{{\sqrt x + 2}} + \dfrac{2}{{\sqrt x - 2}} ( với x > 0; x \ne 4 )

a) Tính giá trị của biểu thức A khi x = 25

b) Rút gọn biểu thức B

c) Tìm các giá trị nguyên của x để B:A > \dfrac{1}{4}

Câu 3: Cho hàm số y = x + 4 \left( {{d_1}} \right)

a) Vẽ đồ thị hàm số trên

b) Xác định tọa độ giao điểm của \left( {{d_1}} \right) với đường thẳng \left( {{d_2}} \right):y = - x - 2

c) Cho đường thẳng \left( {{d_3}} \right):y = \left( {{m^2} - 4} \right)x + 7  . Tìm m để 3 đường thẳng \left( {{d_1}} \right) , \left( {{d_2}} \right), \left( {{d_3}} \right)

đồng quy

Câu 4: Cho (O; R), từ điểm S ở ngoài đường tròn (O; R) sao cho OS = 2R., kẻ hai tiếp tuyến SA, SB với đường tròn ( A, B là tiếp điểm), gọi H là giao điểm của SO và AB

a) Chứng minh:  SO \bot AB

b) Chứng minh: OH.\,\,OS = {R^2}

c) Chứng minh tam giác SBA đều

d) Vẽ cát tuyến SMN của (O;R), xác định vị trí của cát tuyến SMN để SM + SN đạt giá trị nhỏ nhất

Câu 5: Tìm a, b > 0 sao cho:

\left( {{a^2} + b + \dfrac{3}{4}} \right) + \left( {{b^2} + a + \dfrac{3}{4}} \right) - \left( {2a + \dfrac{1}{2}} \right)\left( {2b + \dfrac{1}{2}} \right) = 0

B. Đáp án Đề thi Toán kì 1 lớp 9

Câu 1

1)

a)

\begin{array}{l} \sqrt {20} - \sqrt {80} + 2\sqrt {45} \\ = 2\sqrt 5 - 4\sqrt 5 + 2.3\sqrt 5 \\ = 2\sqrt 5 - 4\sqrt 5 + 6\sqrt 5 \\ = 4\sqrt 5 \end{array}

b)

\begin{array}{l} \dfrac{1}{{3 - \sqrt 7 }} - \dfrac{1}{{3 + \sqrt 7 }}\\ = \dfrac{{3 + \sqrt 7 }}{{\left( {3 - \sqrt 7 } \right)\left( {3 + \sqrt 7 } \right)}} - \dfrac{{3 - \sqrt 7 }}{{\left( {3 + \sqrt 7 } \right)\left( {3 - \sqrt 7 } \right)}}\\ = \dfrac{{3 + \sqrt 7 }}{2} - \dfrac{{3 - \sqrt 7 }}{2}\\ = \dfrac{{3 + \sqrt 7 - 3 + \sqrt 7 }}{2} = \sqrt 7 \end{array}

2) 

\begin{array}{l} \sqrt {25x + 25} - \sqrt {9x + 9} + \sqrt {4x + 4} = 16\\ \Leftrightarrow \sqrt {25\left( {x + 1} \right)} - \sqrt {9\left( {x + 1} \right)} + \sqrt {4\left( {x + 1} \right)} = 16\\ \Leftrightarrow 5\sqrt {\left( {x + 1} \right)} - 3\sqrt {\left( {x + 1} \right)} + 2\sqrt {\left( {x + 1} \right)} = 16\\ \Leftrightarrow 4\sqrt {\left( {x + 1} \right)} = 16\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {ĐK :x + 1 \ge 0 \Leftrightarrow x \ge - 1} \right)\\ \Leftrightarrow \sqrt {\left( {x + 1} \right)} = 4\\ \Leftrightarrow x + 1 = 16\\ \Leftrightarrow x = 15\,\,\left( {t/m} \right) \end{array}

Vậy phương trình có nghiệm x = 15

3)

\left\{ \begin{array}{l} x + y = 3\\ 4x - y = 2 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} 5x = 5\\ x + y = 3 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x = 1\\ y = 3 - 1 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x = 1\\ y = 2 \end{array} \right.

Vậy hệ phương trình có nghiệm ( x, y)  = (1, 2)

Câu 2

a) Khi x = 25 thay vào A ta được:

A = \dfrac{{4\sqrt x }}{{\,\sqrt x - 2}} = \dfrac{{4\sqrt {25} }}{{\,\sqrt {25} - 2}} = \dfrac{{4.5}}{{\,5 - 2}} = \dfrac{{20}}{3}

b) 

\begin{array}{l} B = \dfrac{{2\left( {\sqrt x - 2} \right)}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}} + \dfrac{{2\left( {\sqrt x + 2} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\\ B = \dfrac{{2\sqrt x - 4}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}} + \dfrac{{2\sqrt x + 4}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\\ B = \dfrac{{2\sqrt x - 4 + 2\sqrt x + 4}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}}\\ B = \dfrac{{4\sqrt x }}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}} \end{array}

c) 

Ta có:

\begin{array}{l} B:A = \dfrac{{4\sqrt x }}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}}:\dfrac{{4\sqrt x }}{{\,\sqrt x - 2}}\\ B:A = \dfrac{{4\sqrt x }}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}}.\dfrac{{\,\sqrt x - 2}}{{4\sqrt x }}\\ B:A = \dfrac{1}{{\left( {\sqrt x + 2} \right)}} \end{array}

Để B:A > \dfrac{1}{4} thì

\begin{array}{l} B:A = \dfrac{1}{{\left( {\sqrt x + 2} \right)}} > \dfrac{1}{4}\\ \Leftrightarrow \dfrac{1}{{\left( {\sqrt x + 2} \right)}} - \dfrac{1}{4} > 0\\ \Leftrightarrow \dfrac{4}{{4.\left( {\sqrt x + 2} \right)}} - \dfrac{{\sqrt x + 2}}{{4.\left( {\sqrt x + 2} \right)}} > 0\\ \Leftrightarrow \dfrac{{4 - \sqrt x - 2}}{{4.\left( {\sqrt x + 2} \right)}} > 0\\ \Leftrightarrow \dfrac{{2 - \sqrt x }}{{4.\left( {\sqrt x + 2} \right)}} > 0 \end{array}

Ta có 4.\left( {\sqrt x + 2} \right) > 0\,\,\,\left( {\forall x} \right)

Vậy để B:A > \dfrac{1}{4}  thì 2 - \sqrt x > 0 \Leftrightarrow x < 4

Kết hợp với điều kiện ta được 0 < x < 4

Câu 3:

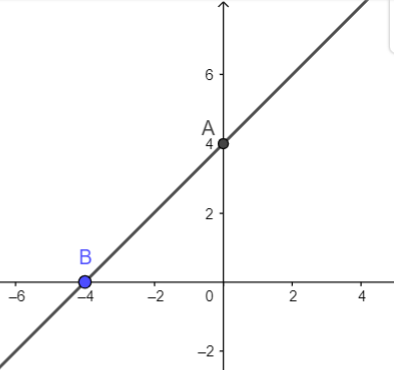
a) 

Giao của đồ thị hàm số với trục Ox là A\left( { - 4;0} \right)

Giao của đồ thị hàm số với trục Oy là B\left( {0;4} \right)

Đồ thị hàm số của đường thẳng y = x + 4 là

b) Gọi M ( x; y) là tọa độ giao điểm của \left( {{d_1}} \right) và \left( {{d_2}} \right)

Tọa độ điểm M là nghiệm của hệ phương trình: \left\{ \begin{array}{l} y = x + 4\\ y = - x - 2 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} 2x + 6 = 0\\ y = x + 4 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x = - 3\\ y = 1 \end{array} \right.

Vậy M ( - 1; 3)

c)

Để 3 đường thẳng \left( {{d_1}} \right) , \left( {{d_2}} \right) , \left( {{d_3}} \right)  đồng quy thì:  M \in \left( {{d_3}} \right) . Thay M vào ta được:

\begin{array}{l} 1 = \left( {{m^2} - 4} \right).\left( { - 3} \right) + 7\\ \Leftrightarrow 1 = - 3{m^2} + 12 + 7\\ \Leftrightarrow 3{m^2} = 12 + 7 - 1\\ \Leftrightarrow 3{m^2} = 18\\ \Leftrightarrow {m^2} = 6\\ \Leftrightarrow \left[ \begin{array}{l} m = \sqrt 6 \\ m = - \sqrt 6 \end{array} \right. \end{array}

Vậy m = \sqrt 6 hoặc m = - \sqrt 6  thì 3 đường thẳng trên đồng quy

Câu 4

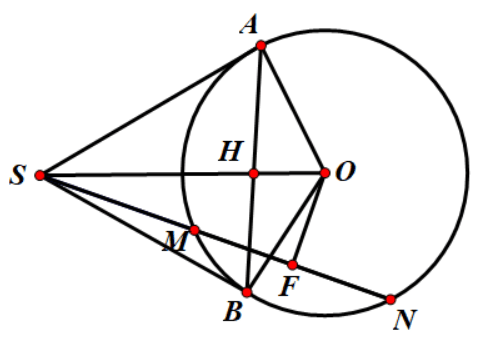
a)

Xét tam giác OAB có

OA = OB = R

\Rightarrow \DeltaOAB cân tại O

Mà  \widehat {BOS} = \widehat {AOS} ( tính chất 2 tiếp tuyến cắt nhau)

Nên OH là đường phân giác

\RightarrowOH là đường cao ( đường phân giác đồng thời là đường cao)

\Rightarrow OH \bot AB

b)

Xét tam giác SAO vuông tại O có:

OH.\,OS = O{A^2}

Mà OA = R

\Rightarrow OH.OS = {R^2}

c)

Xét tam giác SAO vuông tại A có:

\begin{array}{l} \sin \widehat {ASO} = \dfrac{{OA}}{{OS}} = \dfrac{R}{{2R}} = \dfrac{1}{2}\\ \Rightarrow \widehat {ASO} = {30^ \circ } \end{array}

Mà  \widehat {ASB} = 2.\,\widehat {ASO} = {2.30^ \circ } = {60^ \circ }( tính chất 2 tiếp tuyến cắt nhau) (1)

Lại có:

SA = SB ( tính chất 2 tiếp tuyến cắt nhau) (2)

Từ (1) và (2) ta được \Delta SAB  là tam giác đều

d)

Gọi F là trung điểm của MN \Rightarrow OF \bot MN ( đường kính đi qua trung điểm 1 dây)

Ta có:

SM + SN = SF – MF + SF + FN = 2. SF

Mà

\begin{array}{l} S{F^2} = S{O^2} - O{F^2}\\ = {\left( {2R} \right)^2} - O{F^2}\\ = 4{R^2} - O{F^2} \end{array}

OF \le R \Leftrightarrow O{F^2} \le {R^2}

Do đó:

\begin{array}{l} S{F^2} = 4{R^2} - O{F^2} \ge 4{R^2} - {R^2} = 3{R^2}\\ \Leftrightarrow SF \ge \sqrt 3 R \Leftrightarrow SM + SN \ge 2\sqrt 3 R \end{array}

Dấu “ =” xảy ra khi OF = R

Nên cát tuyến SMN trùng với tiếp tuyến SA hoặc SB

Câu 5

Áp dụng BĐT Cô – si cho hai số không âm ta được

\begin{array}{l} {a^2} + \dfrac{1}{4} \ge 2\sqrt {{a^2}.\dfrac{1}{4}} = a\\ {a^2} + b + \dfrac{3}{4} \ge a + b + \dfrac{1}{2} > 0 \end{array}

Tương tự ta chứng minh được:

\Rightarrow \left( {{a^2} + b + \dfrac{3}{4}} \right)\left( {{b^2} + a + \dfrac{3}{4}} \right) \ge {\left( {a + b + \dfrac{1}{2}} \right)^2}

\Rightarrow \left( {{a^2} + b + \dfrac{3}{4}} \right)\left( {{b^2} + a + \dfrac{3}{4}} \right) \ge {\left( {a + b + \dfrac{1}{2}} \right)^2}

Dấu “ =” xảy ra khi a = b = \dfrac{1}{2}

Tương tự ta có

\begin{array}{l} \sqrt {\left( {2a + \dfrac{1}{2}} \right)\left( {2b + \dfrac{1}{2}} \right)} \le \dfrac{1}{2}\left( {2a + \dfrac{1}{2} + 2b + \dfrac{1}{2}} \right)\\ \Rightarrow \left( {2a + \dfrac{1}{2}} \right)\left( {2b + \dfrac{1}{2}} \right) \le {\left( {a + b + \dfrac{1}{2}} \right)^2} \end{array}

Dấu “ =’’ xảy ra khi  2a + \dfrac{1}{2} = 2b + \dfrac{1}{2}hay a = b 

Vậy

\begin{array}{l} \left( {{a^2} + b + \dfrac{3}{4}} \right) + \left( {{b^2} + a + \dfrac{3}{4}} \right) - \left( {2a + \dfrac{1}{2}} \right)\left( {2b + \dfrac{1}{2}} \right) = 0\\ \Leftrightarrow a = b = \dfrac{1}{2} \end{array}

Tài liệu liên quan

Trên đây là giaitoan.com giới thiệu tới quý thầy cô và bạn đọc Đề thi học kì 1 Toán 9 năm học 2022 – 2023 - Đề số 8. Ngoài ra giaitoan.com mời độc giả tham khảo thêm tài liệu ôn tập một số môn học: Toán lớp 9, Giải Toán 9, Đề thi học kì 1 Toán 9, ....

  • 138 lượt xem
Chia sẻ bởi: Lê Thị Thùy
Tìm thêm: Toán 9 Đề thi học kì 1
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan