Đề thi học kì 1 Toán 9 năm học 2022 – 2023 - Đề số 4 Đề thi cuối kì 1 lớp 9
Đề thi học kì 1 Toán 9 năm học 2022 – 2023 - Đề số 4
Đề thi học kì 1 Toán 9 năm học 2022 – 2023 - Đề số 4 được giaitoan.com biên soạn bao gồm các dạng bài tập và đáp án chi tiết được xây dựng theo trọng tâm chương trình học môn Toán lớp 9 giúp học sinh ôn tập, củng cố kiến thức, giúp định vị khả năng tư duy logic, khả năng nhận biết để hoàn thành tốt bài thi cuối học kỳ 1 . Mời các bạn cùng tham khảo chi tiết.
A. Đề thi Toán kì 1 lớp 9
Câu 1
1. Thực hiện phép tính
| a) | b) |
2. Giải phương trình sau: ![]()
Câu 2
Với ![]() cho các biểu thức
cho các biểu thức  và
và 
a) Tính giá trị của biểu thức A biết x = 16
b) Chứng minh rằng 
c) Tìm giá trị của x để nhận giá trị nguyên
Câu 3: Cho hàm số y = ( m – 1) x +4 ( m là tham số, ) có đồ thị hàm số là đường thẳng (d). Tìm m để khoảng cách từ gốc tọa độ đến đường thẳng (d) bằng 2
Câu 4: Cho nửa đường tròn (O) bán kính AB = 2R. Trên nửa mặt phẳng bờ AB chứa nửa đường tròn kẻ hai tia tiếp tuyến Ax, By của nửa đường tròn. Lấy điểm C bất kì thuộc nửa đường tròn ( C khác A và B), qua C kẻ tiếp tuyến của nửa đường tròn cắt Ax, By thứ tự tại M và N
a) Chứng minh A, M, C, O cùng thuộc một đường tròn
b) Nối điểm O với điểm M. điểm O với điểm N. Chứng minh ![]()
c) Chứng minh: AM + NB = MN
Câu 5: Cho ![]() và a.b.c = 1152. Tìm GTLN của biểu thức:
và a.b.c = 1152. Tìm GTLN của biểu thức:
![]()
B. Đáp án Đề thi Toán kì 1 lớp 9
Câu 1
a)

b)

Câu 2
a)
Khi x = 16 thay vào A ta được:

b)

c)

Ta có:

Để Q nhận giá trị nguyên thì ![]()
Với ![]()
Với ![]()
Với ![]()
Với ![]()
Với ![]()
Với ![]()
Vậy để Q nguyên thì ![]()
Câu 3
Giao của đồ thị hàm số với trục Ox là: 

Giao của đồ thị hàm số với trục Oy là: ![]()
Nối A với B ta được tam giác OAB vuông tại O
Khoảng cách từ gốc tọa độ đến đường (d) là OH = 2
Theo hệ thức lượng trong tam giác vuông ta được:

Câu 4
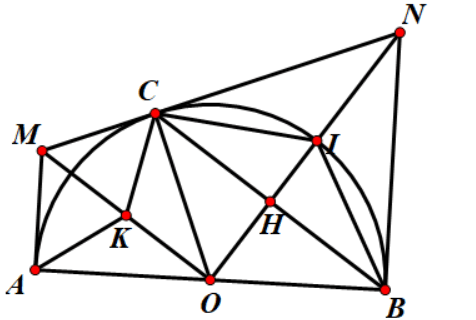
a)
Gọi K là trung điểm của MO ![]() (1)
(1)
Xét tam giác AMO vuông tại A có:
![]() ( tính chất đường trung tuyến của tam giác vuông) (2)
( tính chất đường trung tuyến của tam giác vuông) (2)
Từ (1) và (2) ![]() (*)
(*)
Xét tam giác MCO vuông tại C có:
![]() ( tính chất đường trung tuyến của tam giác vuông) (3)
( tính chất đường trung tuyến của tam giác vuông) (3)
Từ (1) và (3) ![]() (**)
(**)
Từ (*) và (**) ta được
MK = MO = AK = CK ![]() A, M, O, C cùng thuộc 1 đường tròn
A, M, O, C cùng thuộc 1 đường tròn
b)
Ta có:
 ( tiếp tuyến tại A và C cắt nhau tại M)
( tiếp tuyến tại A và C cắt nhau tại M)
Lại có:
 ( tiếp tuyến tại C và B cắt nhau tại N)
( tiếp tuyến tại C và B cắt nhau tại N)
Mà :

![]() vuông tại O
vuông tại O
Áp dụng hệ thức lượng trong tam giác NOM có:

c)
Ta có: MN = MC + NC (4)
Mà: MC = AM ( tính chất 2 tiếp tuyến cắt nhau)
CN = NB ( tính chất 2 tiếp tuyến cắt nhau)
Thay vào (4) ta được: MN = AM + NB
Câu 5
Với ![]() .
.
Áp dụng BĐT Cô – si ta được:
![]()
Chứng minh tương tự ta được:
![]()
![]()

Dấu “=” xảy ra khi 
Vậy ![]() khi a = 2; b = 18; c = 32
khi a = 2; b = 18; c = 32
Tài liệu liên quan
- Đề thi học kì 1 Toán 9 năm học 2022 – 2023 - Đề số 2
Đề thi học kì 1 Toán 9 năm học 2022 – 2023 - Đề số 1
Đề thi học kì 1 Toán 9 năm học 2022 – 2023 - Đề số 3
Đề thi học kì 1 Toán 9 năm học 2022 – 2023 - Đề số 5
Trên đây là giaitoan.com giới thiệu tới quý thầy cô và bạn đọc Đề thi học kì 1 Toán 9 năm học 2022 – 2023 - Đề số 4. Ngoài ra giaitoan.com mời độc giả tham khảo thêm tài liệu ôn tập một số môn học: Toán lớp 9, Giải Toán 9, Đề thi học kì 1 Toán 9, ....




























