Giaitoan.com Toán 10 Giải Toán 10 CTST Tập 1

Cho bất phương trình 2x – y + 1 < 0 Giải Toán 10 Chân trời sáng tạo

Nội dung
  • 1 Đánh giá

Hoạt động 3 trang 30 Toán 10 tập 1

Giải SGK Toán 10: Hoạt động 3 trang 30 Giải bất phương trình bậc nhất hai ẩn được GiaiToan hướng dẫn giúp các học sinh luyện tập về dạng bài tính nhanh. Hi vọng tài liệu này giúp các em học sinh tự củng cố kiến thức, luyện tập và nâng cao cách giải bài tập Toán lớp 10. Mời các em cùng các thầy cô tham khảo.

Cho bất phương trình 2x – y + 1 < 0

a) Vẽ đường thẳng y = 2x + 1

b) Các cặp số (-2; 0), (0; 0), (1; 1) có là nghiệm của bất phương trình đã cho không?

Lời giải chi tiết

a) Hình vẽ minh họa đường thẳng y = 2x + 1

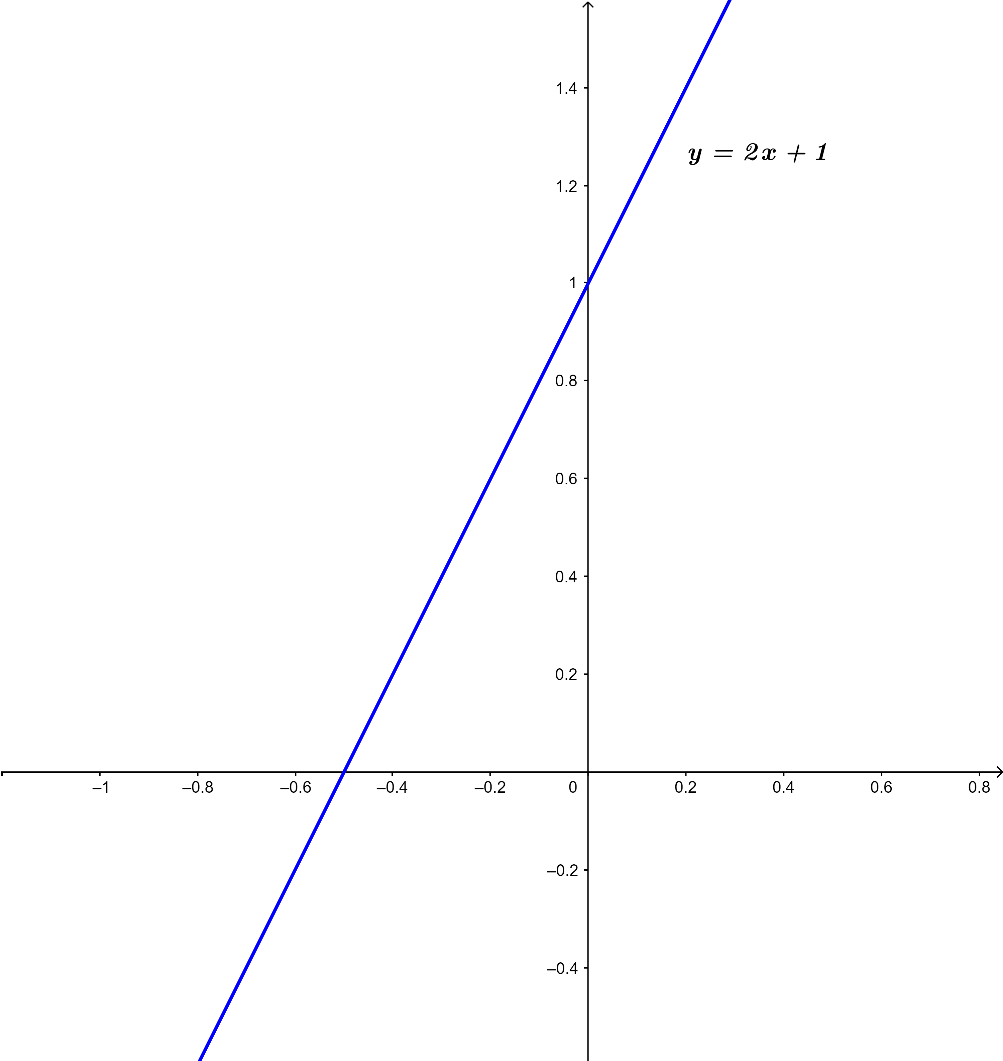
Cho bất phương trình 2x – y + 1 < 0

b) Gọi ∆’: 2x – y + 1 = 0

Xét gốc tọa độ O(0 ; 0)

Ta thấy O ∉ ∆’ và 2.0 - 0 +1 = 1 > 0

=> (0; 0) là không nghiệm của bất phương trình 2x – y + 1 < 0

Xét điểm (-2; 0)

Ta thấy (-2; 0) ∉ ∆’ và -2.2 - 0 +1 = -3 < 0

=> (-2; 0) là nghiệm của bất phương trình 2x – y + 1 < 0

Xét điểm (1; 1)

Ta thấy (1; 1) ∉ ∆’ và 1.2 - 1 + 1 = 2 > 0

=> (1; 1) là không nghiệm của bất phương trình 2x – y + 1 < 0

Vậy cặp số (-2; 0) là nghiệm của bất phương trình 2x – y +1 < 0

A. Bất phương trình bậc nhất hai ẩn

- Bất phương trình bậc nhất hai ẩn x, y có dạng tổng quát là:

ax + by ≤ c (ax + by ≥ c, ax + by < c, ax + by > c)

trong đó a, b, c là những số thực đã cho, a và b không đồng thời bằng 0, x và y là các ẩn số.

- Cặp số (x0; y0) được gọi là một nghiệm của bất phương trình bậc nhất hai ẩn ax + by ≤ c nếu bất đẳng thức ax0 + by0 ≤ c đúng.

B. Cách giải bất phương trình

- Các biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn ax + by ≤ c

+ Vẽ đường thẳng d: ax + by = c trên mặt phẳng Oxy

+ Lấy một điểm M0(x0; y0) không thuộc d.

+ Tính ax0 + by0 và so sánh với c

+ Nếu ax0 + by0 < c thì nửa mặt phẳng bờ d chưa M0 là miền nghiệm của bất phương trình. Nếu ax0 + by0 > c thì nửa mặt phẳng bờ d chứa M0 là miền nghiệm của bất phương trình.

----> Bài học liên quan: Toán 10 Bài 1 Bất phương trình bậc nhất hai ẩn

-------------------------------------------------

Ngoài dạng bài tập Chuyên đề Toán 10: Bất phương trình bậc nhất hai ẩn các em học sinh có thể tham khảo thêm nhiều nội dung Hỏi đáp Toán lớp 10 được GiaiToan đăng tải. Với phiếu bài tập này sẽ giúp các em rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các em học tập tốt!

Chia sẻ bởi: Thiên Bình
Mời bạn đánh giá!
  • Lượt xem: 670
Tìm thêm: Toán 10 Bài tập Toán 10
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần