Giaitoan.com Toán 10 Giải Toán 10 CTST Tập 1

Bài 6 trang 39 Toán 10 tập 1 SGK Chân trời sáng tạo Giải Toán 10

Nội dung
  • 1 Đánh giá

Bài 6 trang 39 SGK Toán 10

Toán lớp 10 Bài 6 trang 39 là lời giải bài Bài tập cuối chương 2 trang 39 SGK Toán 10 sách Chân trời sáng tạo hướng dẫn chi tiết lời giải giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải Toán 10. Mời các em học sinh cùng tham khảo chi tiết.

Giải bài 6 Toán 10 trang 39

Bài 6 (SGK trang 39): Một xưởng sản xuất có hai máy đặc chủng A, B sản xuất hai loại sản phẩm X, Y. Để sản xuất một tấn sản phẩm X cần dùng máy A trong 6 giờ và dùng máy B trong 2 giờ. Để sản xuất một tấn sản phẩm Y cần dùng máy A trong 2 giờ và dùng máy B trong 2 giờ. Cho biết mỗi máy không thể sản xuất đồng thời hai loại sản phẩm. Máy A làm việc không quá 12 giờ một ngày; máy B làm việc không quá 8 giờ một ngày. Một tấn sản phẩm X lãi 10 triệu đồng và một tấn sản phẩm Y lãi 8 triệu đồng. Hãy lập kế hoạch sản xuất mỗi ngày sao cho tổng số tiền lãi cao nhất.

Hướng dẫn giải

- Trong mặt phẳng tọa độ, tập hợp các điểm có tọa độ là nghiệm của hệ bất phương trình bậc nhất hai ẩn là miền nghiệm của hệ bất phương trình đó.

- Miền nghiệm của hệ là giao các miền nghiệm của các bất phương trình trong hệ.

- Cách xác định miền nghiệm của một hệ bất phương trình bậc nhất hai ẩn:

+ Trên cùng một mặt phẳng tọa độ, xác định miền nghiệm của mỗi bất phương trình bậc nhất hai ẩn trong hệ và gạch bỏ miền còn lại.

+ Miền không bị gạch là miền nghiệm của hệ bất phương trình đã cho.

Lời giải chi tiết

Gọi x (tấn) là khối lượng sản phẩm X mà xưởng sản xuất ra trong một ngày; y(tấn) là khối lượng sản phẩm Y mà xưởng sản xuất ra trong một ngày.

Hiển nhiên x ≥ 0 và y ≥ 0.

Để sản xuất x tấn sản phẩm X cần dùng máy A trong 6x (giờ) ; để sản xuất y tấn sản phẩm Y cần dùng máy A trong 2y (giờ).

Tổng số giờ dùng máy A trong một ngày là 6x + 2y (giờ).

Để sản xuất x tấn sản phẩm X cần dùng máy B trong 2x (giờ) ; để sản xuất y tấn sản phẩm Y cần dùng máy B trong 2y (giờ).

Tổng số giờ dùng máy B trong một ngày là 2x + 2y (giờ).

Do máy B làm việc không quá 8 giờ một ngày nên ta có bất phương trình: 2x + 2y ≤ 8 => x + y ≤ 4

=> Ta có hệ bất phương trình: \left\{ {\begin{array}{*{20}{c}} {x \geqslant 0} \\ {y \geqslant 0} \\ \begin{gathered} 3x + y \leqslant 6 \hfill \\ x + y \leqslant 4 \hfill \\ \end{gathered} \end{array}} \right.

Miền nghiệm của hệ trên mặt phẳng tọa độ Oxy ta được biểu diễn như sau:

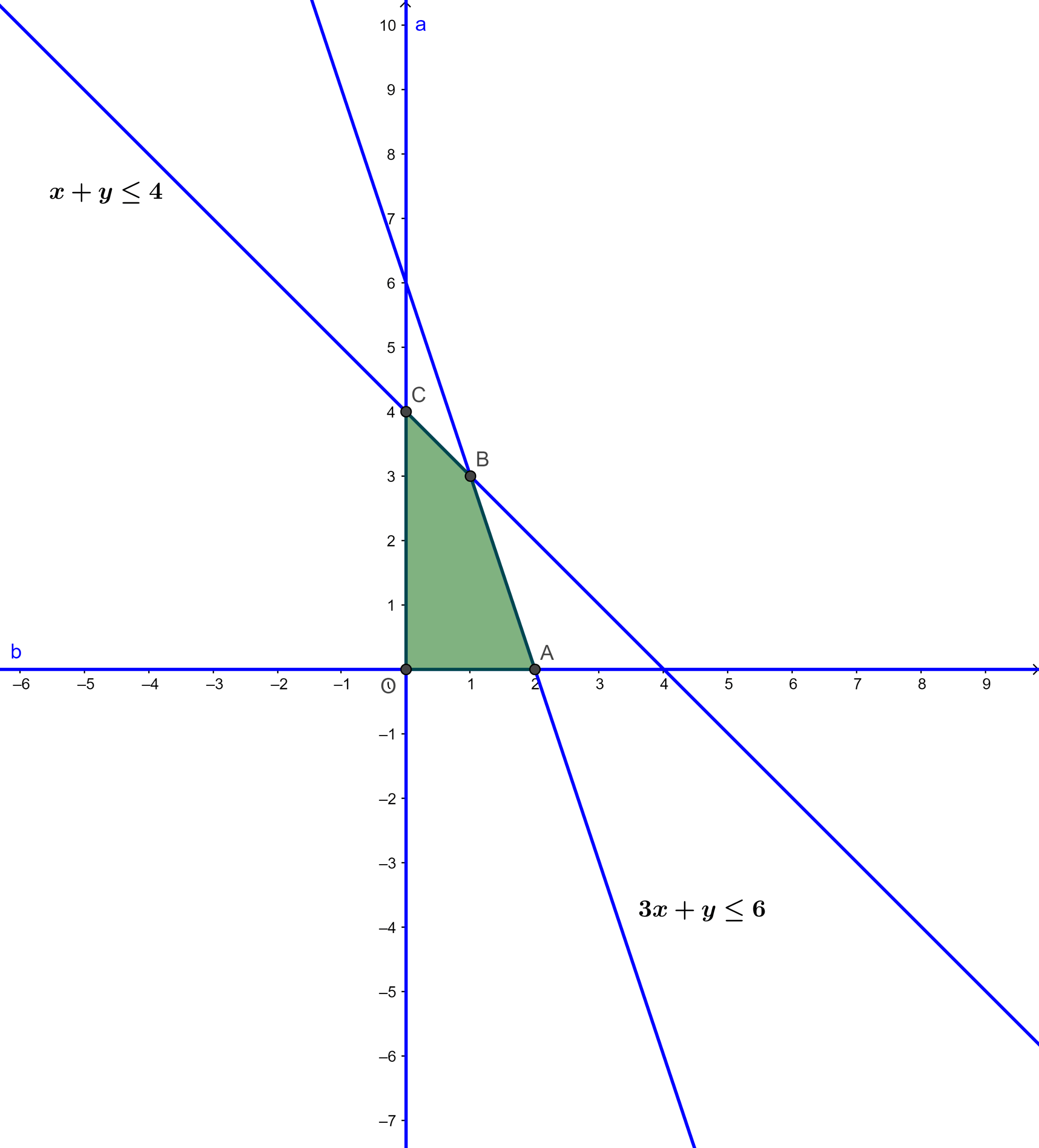
Bài 6 trang 39 Toán 10 tập 1 SGK Chân trời sáng tạo

Miền nghiệm của hệ là miền tứ giác OABC (bao gồm cả các cạnh) với các đỉnh O(0; 0), A (2; 0), B(1; 3), C(0; 4).

Gọi T (triệu đồng) là số tiền lãi thu được.

Với x tấn sản phẩm X thì số tiền lãi là 10x (triệu đồng); với y tấn sản phẩm Y thì số tiền lãi là 8y (triệu đồng).

=> Tổng số tiền lãi là 10x + 8y (triệu đồng).

=> T =10x + 8y

Tính giá trị của T tại các đỉnh của tứ giác OABC:

Tại O (0; 0) => T= 10.0 + 8.0 = 0

Tại A (2; 0) => T = 10.2 + 8.0 = 20

Tại B(1; 3) => T = 10.1 + 8.3 = 34

Tại C(0; 4) => T = 10.0 + 8.4 = 32

=> T đạt giá trị lớn nhất là 34 tại B(1; 3)

Vậy để tổng số tiền lãi cao nhất thì xưởng phải sản xuất 1 tấn sản phẩm X và 3 tấn sản phẩm Y.

------> Bài liên quan: Giải Toán 10 Bài tập cuối chương 2 trang 39

----------------------------------------

Trên đây là lời giải chi tiết Bài 6 Toán lớp 10 trang 39 Bài tập cuối chương 2 trang 39 cho các em học sinh tham khảo, nắm được cách giải các dạng toán của Chương 2: Bất phương trình và hệ bất phương trình bậc nhất hai ẩn . Hi vọng đây là tài liệu hữu ích cho các bạn ôn tập kiểm tra năng lực, bổ trợ cho quá trình học tập trong chương trình THPT cũng như ôn luyện cho kì thi THPT Quốc gia. Chúc các bạn học tốt!

Ngoài ra mời bạn đọc tham khảo thêm một số tài liệu: Giải Toán 10 sách CTST, Giải Toán 10 sách Cánh Diều, Hỏi đáp Toán 10

Chia sẻ bởi: Đen2017
Mời bạn đánh giá!
  • Lượt xem: 1.042
Tìm thêm: Toán 10 Giải Toán 10
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần