Giaitoan.com Toán 10 Giải Toán 10 CTST Tập 1

Bài 1 trang 93 Toán 10 tập 1 SGK Chân trời sáng tạo Giải Toán 10 sách Chân trời sáng tạo

Nội dung
  • 1 Đánh giá

Bài 1 trang 93 SGK Toán 10

Toán lớp 10 Bài 1 trang 93 là lời giải bài Tổng và hiệu của hai vecto SGK Toán 10 sách Chân trời sáng tạo hướng dẫn chi tiết lời giải giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải Toán 10. Mời các em học sinh cùng tham khảo chi tiết.

Giải bài 1 Toán 10 trang 93

Bài 1 (SGK trang 93): Cho hình bình hành ABCD có O là giao điểm của hai đường chéo và một điểm M tùy ý. Chứng minh rằng:

a) \overrightarrow {BA} + \overrightarrow {DC} = \overrightarrow 0

b) \overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MB} + \overrightarrow {MD}

Hướng dẫn giải

- Quy tắc ba điểm: Cho ba điểm M, N, P ta có: \overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MP}

- Nếu OABC là hình bình hành thì ta có: \overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow {OB}

- Phép cộng vecto có tính chất:

+ Giao hoán: \overrightarrow a + \overrightarrow b = \overrightarrow b + \overrightarrow a

+ Kết hợp: \left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c = \overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right)

+ Với mọi vecto \overrightarrow a, ta có: \overrightarrow a + \overrightarrow 0 = \overrightarrow 0 + \overrightarrow a = \overrightarrow a

Lời giải chi tiết

Hình vẽ minh họa:

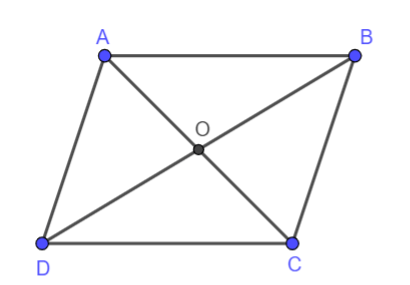
Bài 1 trang 93 Toán 10 tập 1 SGK Chân trời sáng tạo

a) Ta có: ABCD là hình bình hành nên \overrightarrow {AB} = \overrightarrow {DC}

=> \overrightarrow {BA} + \overrightarrow {DC} = \overrightarrow {BA} + \overrightarrow {AB} = \overrightarrow {BB} = \overrightarrow 0

=> \overrightarrow {BA} + \overrightarrow {DC} = \overrightarrow 0

b) Gọi O là giao điểm của hai đường chéo AC và BD của hình bình hành ABCD

=> OA = OC; OB = OD

=> \overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow 0 ;\overrightarrow {OB} + \overrightarrow {OD} = \overrightarrow 0

Ta có:

\begin{matrix} \overrightarrow {MA} + \overrightarrow {MC} = \left( {\overrightarrow {MO} + \overrightarrow {OA} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OC} } \right) \hfill \\ = \overrightarrow {MO} + \overrightarrow {MO} + \left( {\overrightarrow {OC} + \overrightarrow {OA} } \right) \hfill \\ = \overrightarrow {MO} + \overrightarrow {MO} + \overrightarrow 0 = 2\overrightarrow {MO} \left( * \right) \hfill \\ \overrightarrow {MB} + \overrightarrow {MD} = \left( {\overrightarrow {MO} + \overrightarrow {OB} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OD} } \right) \hfill \\ = \overrightarrow {MO} + \overrightarrow {MO} + \left( {\overrightarrow {OD} + \overrightarrow {OB} } \right) \hfill \\ = \overrightarrow {MO} + \overrightarrow {MO} + \overrightarrow 0 = 2\overrightarrow {MO} \left( {**} \right) \hfill \\ \end{matrix}

Từ (*) và (**) => \overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MB} + \overrightarrow {MD}

-----> Câu hỏi tiếp theo: Bài 2 trang 93 SGK Toán 10

----------------------------------------

Trên đây là lời giải chi tiết Bài 1 Toán lớp 10 trang 93 Tổng và hiệu của hai vecto cho các em học sinh tham khảo, nắm được cách giải các dạng toán của Chương 3: Hệ thức lượng trong tam giác . Hi vọng đây là tài liệu hữu ích cho các bạn ôn tập kiểm tra năng lực, bổ trợ cho quá trình học tập trong chương trình THPT cũng như ôn luyện cho kì thi THPT Quốc gia. Chúc các bạn học tốt!

Ngoài ra mời bạn đọc tham khảo thêm một số tài liệu: Giải Toán 10 sách CTST, Giải Toán 10 sách Cánh Diều, Hỏi đáp Toán 10

Chia sẻ bởi: Đường tăng
Mời bạn đánh giá!
  • Lượt xem: 1.966
Tìm thêm: Toán 10 Giải Toán 10
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần