Giaitoan.com Toán 7 Giải Toán 7 tập 2 KNTT

Vận dụng trang 75 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống Giải Toán 7 sách Kết nối tri thức

Nội dung
  • 3 Đánh giá

Vận dụng trang 75 SGK Toán 7 tập 2

Toán 7 tập 2 Vận dụng trang 75 là lời giải bài Sự đồng quy của ba trung tuyến, ba đường phân giác trong một tam giác SGK Toán 7 sách Kết nối tri thức với cuộc sống hướng dẫn chi tiết lời giải giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải Toán 7. Mời các em học sinh cùng tham khảo chi tiết.

Giải Vận dụng Toán 7 trang 75

Vận dụng (SGK trang 75): Chứng minh rằng trong tam giác đều, điểm cách đều ba cạnh của tam giác là trọng tâm của tam giác đó.

Hướng dẫn giải

+ Ba đường trung tuyến của một tam giác cùng đi qua một điểm (hay đồng quy tại một điểm). Điểm đó cách mỗi đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy.

+ Ba đường phân giác của một tam giác đồng quy tại một điểm. Điểm này cách đều ba cạnh của tam giác đó.

Lời giải chi tiết

Hình vẽ minh họa:

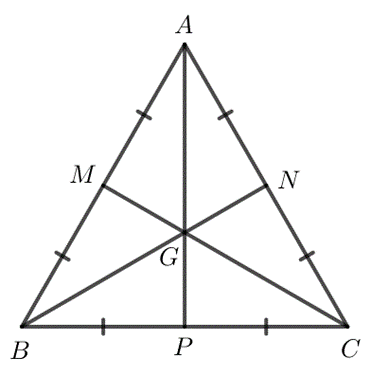
Vận dụng trang 75 Toán 7 tập 2 SGK Kết nối tri thức với cuộc sống

Giả sử tam giác ABC là tam giác đều có M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC và G là trọng tâm của tam giác.

Khi đó A, G, P thẳng hàng; B, G, N thẳng hàng; C, G, M thẳng hàng

Ta có: Tam giác ABC đều => \left\{ {\begin{array}{*{20}{c}} {AB = BC = AC} \\ {\widehat {ABC} = \widehat {BAC} = \widehat {ACB}} \end{array}} \right.

Xét tam giác APB và tam giác APC có:

AB = AC

AP chung

PB = PC

=> ∆APB = ∆APC (c – c - c)

=> \widehat {APB} = \widehat {APC} (Hai góc tương ứng)

Mà \widehat {APB} + \widehat {APC} = {180^0} \Rightarrow \widehat {APB} = \widehat {APC} = {90^0}

=> AP ⊥ BC hay GP ⊥ BC.

=> GP là khoảng cách từ G đến BC.

Chứng minh tương tự ta có GM, GN lần lượt là khoảng cách từ G đến AC, AC.

Do M là trung điểm của AB => MB = \frac{1}{2}AB

Do N là trung điểm của AC => NC = \frac{1}{2}AC

Mà AB = AC nên MB = NC

Xét tam giác MBC và tam giác NCB có:

MB = NC

\widehat {MBC} = \widehat {NCB}

BC chung

=> ∆MBC = ∆NCB (c – g - c)

=> CM = BN (Hai cạnh tương ứng)

Tam giác ABC có G là trọng tâm

=> \left\{ {\begin{array}{*{20}{c}} {CG = \dfrac{2}{3}CM} \\ {BG = \dfrac{2}{3}BN} \end{array}} \right. \Rightarrow GM = \dfrac{1}{3}CM;GN = \dfrac{1}{3}BN

Mà CM = BN => GM = GN

Chứng minh tương tự ta có GM = GN = GP

Khi đó trọng tâm G của tam giác đều ABC cách đều ba cạnh của tam giác.

Vậy trong tam giác đều, điểm cách đều ba cạnh của tam giác là trọng tâm của tam giác đó.

----> Câu hỏi tiếp theo: Bài 9.20 trang 76 SGK Toán 7 tập 2

----------------------------------------

Trên đây là lời giải chi tiết Vận dụng Toán 7 trang 75 Sự đồng quy của ba trung tuyến, ba đường phân giác trong một tam giác cho các em học sinh tham khảo, nắm được cách giải các dạng toán của Chương 9: Quan hệ giữa các yếu tố trong một tam giác. Qua đó giúp các em học sinh ôn tập chuẩn bị cho các bài thi giữa và cuối học kì lớp 7. Chúc các em học tốt. Mời thầy cô và học sinh tham khảo thêm tài liệu:  Giải Toán 7 tập 2 KNTT,  Giải Toán 7 Chân trời sáng tạo tập 2,   Giải Toán 7 Tập 2 sách Cánh Diều

Chia sẻ bởi: Khang Anh
Mời bạn đánh giá!
  • Lượt xem: 3.516
Tìm thêm: Toán 7 Giải Toán 7
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần