Giaitoan.com Toán 8 Đề thi giữa kì 1 lớp 8

Đề thi giữa kì 1 môn Toán lớp 8 năm học 2022 - 2023 - Đề số 13 Đề kiểm tra giữa kì 1 Toán 8

Nội dung
  • 1 Đánh giá

Đề thi giữa kì 1 Toán 8 năm học 2022 - 2023 Đề số 13

Đề thi giữa kì 1 Toán 8 năm học 2021 - 2022 Đề số 13 được Giaitoan.com biên soạn bao gồm các dạng bài tập và đáp án chi tiết được xây dựng theo trọng tâm chương trình học THCS giúp học sinh ôn tập, củng cố kiến thức, giúp định vị khả năng tư duy logic, khả năng nhận biết. Đây là nền tảng vững chắc giúp các bạn tự tin làm bài trong các kì thi và kiểm tra định kì môn Toán 8. Mời các bạn cùng tham khảo chi tiết!

A. Đề thi Toán giữa kì 1 lớp 8

Câu 1: Phân tích đa thức thành nhân tử

\begin{array}{l} a)\,\,2{x^3} - 12{x^2} + 18x\\ b)\,\,{x^2} - 4{y^2} + 8x - 16\\ c)\,{\left( {x + 4} \right)^2} + 8x\left( {x + 4} \right) + 15{x^2} \end{array}

Câu 2: Tìm x biết:

\begin{array}{l} a)3x\left( {x - 2022} \right) - x + 2022 = 0\\ b)\,4{x^2} - 8x + 4 = 0 \end{array}

Câu 3: Tìm n để đa thức {x^4} - {x^3} + 6{x^2} - x + n chia hết cho đa thức {x^2} - x + 5

Câu 4: Cho tam giác ABC vuông tại A ( AB < AC ), đường cao AD. Từ D kẻ DE và DF vuông góc với AB và AC. Gọi I và K là trung điểm của DC và KC

a) Tứ giác ADEF là hình gì ? Vì sao?

b) AD cắt EF tại O. Chứng minh OIKC là hình bình hành

Câu 5: Tìm x, y biết: {x^2} + 5{y^2} + 4xy + 6x + 6y + 32 = 0

B. Đáp án Đề thi Toán giữa kì 1 lớp 8

Câu 1: Phân tích đa thức thành nhân tử:

\begin{array}{l} a)\,\,2{x^3} - 12{x^2} + 18x\\ b)\,\,{x^2} - 4{y^2} + 8x - 16\\ c)\,{\left( {x + 4} \right)^2} + 8x\left( {x + 4} \right) + 15{x^2} \end{array}

Hướng dẫn giải

\begin{array}{l} a)\,\,2{x^3} - 12{x^2} + 18x\\ = 2x\left( {{x^2} - 6x + 9} \right) = 2x{\left( {x - 3} \right)^2}\\ b)\,\,{x^2} - 4{y^2} + 8x - 16y\\ = \left( {{x^2} - 4{y^2}} \right) + 8\left( {x - 2y} \right)\\ = \left( {x - 2y} \right)\left( {x + 2y} \right) + 8\left( {x - 2y} \right)\\ = \left( {x - 2y} \right)\left( {x + 2y + 8} \right) \end{array}

c)\,{\left( {x + 4} \right)^2} + 8x\left( {x + 4} \right) + 15{x^2}

Đặt x + 4 = tta được;

{t^2} + 8xt + 15{x^2}

Chia đa thức cho {x^2} ta được

\begin{array}{l} {t^2} + 8xt + 15{x^2} = \dfrac{{{t^2}}}{{{x^2}}} + \dfrac{{8xt}}{{{x^2}}} + \dfrac{{15{x^2}}}{{{x^2}}} = {\left( {\dfrac{t}{x}} \right)^2} + 8\left( {\dfrac{t}{x}} \right) + 15\\ = {\left( {\dfrac{t}{x}} \right)^2} + 5\left( {\dfrac{t}{x}} \right) + 3\left( {\dfrac{t}{x}} \right) + 15\\ = \left( {\dfrac{t}{x}} \right)\left[ {\left( {\dfrac{t}{x}} \right) + 5} \right] + 3\left[ {\left( {\dfrac{t}{x}} \right) + 5} \right]\\ = \left[ {\left( {\dfrac{t}{x}} \right) + 5} \right]\left[ {\left( {\dfrac{t}{x}} \right) + 3} \right]\,\,\,\,\left( * \right) \end{array}

Thay x + 4 = t vào (*) ta được

\begin{array}{l} \left[ {\left( {\dfrac{t}{x}} \right) + 5} \right]\left[ {\left( {\dfrac{t}{x}} \right) + 3} \right]\,\, = \left[ {\left( {\dfrac{{x + 4}}{x}} \right) + 5} \right]\left[ {\left( {\dfrac{{x + 4}}{x}} \right) + 3} \right]\\ = \left( {\dfrac{{x + 4}}{x} + 5} \right)\left( {\dfrac{{x + 4}}{x} + 3} \right)\\ = \left( {\dfrac{{x + 4 + 5x}}{x}} \right)\left( {\dfrac{{x + 4 + 3x}}{x}} \right) = \left( {\dfrac{{4 + 6x}}{x}} \right)\left( {\dfrac{{4x + 4}}{x}} \right) \end{array}

Câu 2: Tìm x biết:

\begin{array}{l} a)3x\left( {x - 2022} \right) - x + 2022 = 0\\ b)\,4{x^2} - 8x + 4 = 0 \end{array}

Hướng dẫn giải

\begin{array}{l} a)\,\,\,3x\left( {x - 2022} \right) - x + 2022 = 0\\ \Leftrightarrow 3x\left( {x - 2022} \right) - \left( {x - 2022} \right) = 0\\ \Leftrightarrow \left( {x - 2022} \right)\left( {3x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l} x - 2022 = 0\\ 3x - 1 = 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = 2022\\ x = \frac{1}{3} \end{array} \right. \end{array}

Vậy phương trình có nghiệm x = 2022 hoặc x = \dfrac{1}{3}

\begin{array}{l} b)\,4{x^2} - 8x + 4 = 0\\ \Leftrightarrow 4\left( {{x^2} - 2x + 1} \right) = 0\\ \Leftrightarrow \left( {{x^2} - 2x + 1} \right) = 0\\ \Leftrightarrow {\left( {x - 1} \right)^2} = 0\\ \Leftrightarrow x = 1 \end{array}

Vậy phương trình có nghiệm x = 1

Câu 3: Tìm n để đa thức {x^4} - {x^3} + 6{x^2} - x + n chia hết cho đa thức {x^2} - x + 5

Hướng dẫn giải

{x^4} - {x^3} + 6{x^2} - x + n = {x^4} - {x^3} + 5{x^2} + {x^2} - x + n = {x^2}\left( {{x^2} - x + 5} \right) + {x^2} - x + n

Để đa thức {x^4} - {x^3} + 6{x^2} - x + n chia hết cho đa thức  {x^2} - x + 5  thì

{x^2}\left( {{x^2} - x + 5} \right) + {x^2} - x + n\,\, \vdots \,\,\,{x^2} - x + 5 \Rightarrow n = 5

Câu 4: Cho tam giác ABC vuông tại A ( AB < AC ), đường cao AD. Từ D kẻ DE và DF vuông góc với AB và AC. Gọi I và K là trung điểm của DC và KC

a) Tứ giác ADEF là hình gì ? Vì sao?

b) AD cắt EF tại O. Chứng minh OIKC là hình bình hành

Hướng dẫn giải

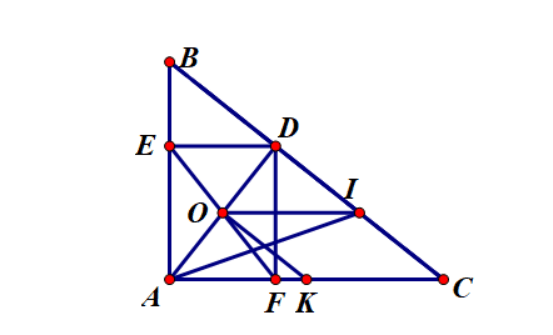
a) Xét tứ giác ADEF có:

\widehat {ABC} = \,\widehat {DEA} = \widehat {DFA} = {90^ \circ }

Vậy tứ giác ADEF là hình chữ nhật

b) Ta có OA = OD ( tính chất hình chữ nhật ABCD)

ID = IC ( I là trung điểm của DC )

Nên OI là đường trung bình của tam giác ADC

\Rightarrow \left\{ \begin{array}{l} OI//BC\\ OI = \dfrac{1}{2}BC \end{array} \right.

Mà KA = KC ( K là trung điểm của AC )

Nên \Rightarrow \left\{ \begin{array}{l} OI//BC \Rightarrow \,\,OI//KC\\ OI = KC \end{array} \right. \Rightarrow OIKC là hình bình hành

Câu 5: Tìm x, y biết:  {x^2} + 5{y^2} + 4xy + 6x + 6y + 32 = 0

Hướng dẫn giải

\begin{array}{l} {x^2} + 5{y^2} + 4xy + 6x + 6y + 9 = 0\\ \Leftrightarrow {x^2} + 4xy + 4{y^2} + 6y + 6x + 9 + {y^2} = 0\\ \Leftrightarrow {\left( {x + 2y + 3} \right)^2} + {y^2} = 0 \end{array}

Ta có:

\begin{array}{l} {\left( {x + 2y + 3} \right)^2} \ge 0\,\,\,\,\,\,\,\left( {\forall x,y} \right)\\ {y^2} \ge 0\,\,\,\,\,\,\,\left( {\forall y} \right)\\ \Rightarrow {\left( {x + 2y + 3} \right)^2} + {y^2} \ge 0\,\,\,\,\left( {\forall x,y} \right) \end{array}

Dấu “ =’’ xảy ra khi: \left\{ \begin{array}{l} {\left( {x + 2y + 3} \right)^2} = 0\,\\ {y^2} = 0\, \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x + 2y + 3 = 0\,\\ y = 0\, \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x = - 3\,\\ y = 0\, \end{array} \right.

Tài liệu liên quan:

Đề thi giữa kì 1 Toán 8 năm học 2022 - 2023 Đề số 11
Đề thi giữa kì 1 Toán 8 năm học 2022 - 2023 Đề số 12
Đề kiểm tra giữa học kì 1 môn Toán lớp 8 năm học 2022 - 2023 Đề 11
Đề kiểm tra giữa học kì 1 môn Toán lớp 8 năm học 2022 - 2023 Đề 12

Trên đây Giaitoan.com giới thiệu tới quý thầy cô và bạn đọc tài liệu Đề kiểm tra giữa học kì 1 môn Toán 8 năm học 2022 - 2023 Đề 13. Ngoài ra học sinh có thể tham khảo thêm một số tài liệu liên quan: Lý thuyết Toán 8, Luyện tập Toán 8, Giải Toán 8 Tập 1, ....

  • 63 lượt xem
Chia sẻ bởi: Lê Thị Thùy
Tìm thêm: Toán 8 Đề thi học kì lớp 8
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan