Đề kiểm tra giữa học kì 1 môn Toán lớp 7 - Đề 2 Đề kiểm tra giữa học kỳ 1 môn Toán lớp 7 có đáp án

65 Đánh giá

Đề thi giữa kì 1 môn Toán lớp 7 - Đề 2

Đề thi giữa học kì I lớp 7 năm 2020 – 2021
Đáp án đề kiểm tra giữa học kì Đề số 2

Đề thi giữa học kì môn Toán lớp 7 năm học 2020 - 2021 - Đề 2 được giaitoan.com biên soạn bao gồm các dạng bài tập và đáp án chi tiết được xây dựng theo trọng tâm chương trình học THCS giúp học sinh ôn tập, củng cố kiến thức, giúp định vị khả năng tư duy logic, khả năng nhận biết. Đây là nền tảng vững chắc giúp các bạn tự tin làm bài trong các kì thi và kiểm tra định kì. Mời các bạn cùng tham khảo chi tiết.

Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 7, giaitoan.com mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm Giải Toán . Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.

Đề thi giữa học kì I lớp 7

Môn: Toán – Đề số 2

Thời gian: 90 phút

Bản quyền thuộc về GiaiToan.
Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại.

Câu 1 (3 điểm) Thực hiện phép tính (bằng cách hợp lí nếu có thể):

$a. 2\frac{3}{5}+\left( \frac{1}{2}+\frac{5}{3} \right):\frac{5}{6}$	$b. \left( \frac{-5}{7}+\frac{4}{9} \right):\frac{4}{5}+\left( \frac{-2}{7}+\frac{-13}{9} \right):\frac{4}{5}$
$c. \frac{{{2}^{5}}.{{\left( -49 \right)}^{2}}}{{{4}^{5}}{{.7}^{3}}}$	$d. {{\left( \frac{-4}{3} \right)}^{3}}:\frac{{{\left( \dfrac{-1}{3} \right)}^{2}}}{6}$

Câu 2 (2 điểm) Tìm x biết:

$a. \frac{3}{4}-x=\frac{3}{5}$
$b. \frac{1}{4}-\left( \frac{2}{5}+2x \right)=\frac{2}{3}$
$c. 4-\left| x-\frac{1}{5} \right|=\frac{1}{3}$
Câu 3 (2 điểm) Tìm diện tích của hình chữ nhật biết chu vi hình chữ nhật là 60cm, tỉ lệ hai cạnh của hình chữ nhật là 2 : 3.

Câu 4 (3 điểm) Cho hình vẽ, biết đường d song song với đường thẳng d' và góc D₂ bằng 135⁰, góc ADB bằng 60⁰, góc B₂ bằng 165⁰ .

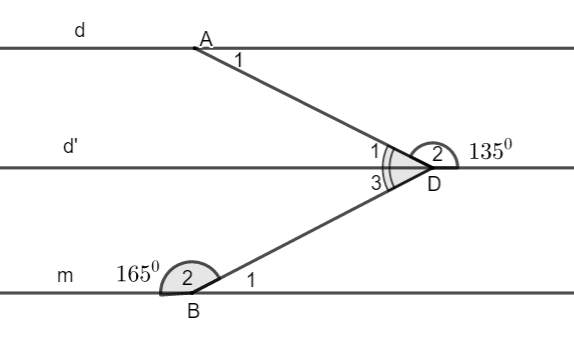Đề kiểm tra giữa học kì 1 môn Toán lớp 7 năm học 2020 - 2021 Đề 2

a. Chứng minh đường thẳng d sông song với đường thẳng m.

b. Tính số đo góc A₁

c. Tính số đo góc D₁, D₃

Câu 5 (1 điểm) Tính giá trị của biểu thức $A=\frac{2x-3y+5z}{4x+5y-2z}$ ,(x, y, z ≠ 0, 4x + 5y - 2z ≠ 0) biết

$\frac{x}{2}=\frac{y}{-3}=\frac{z}{4}$

Đáp án đề kiểm tra giữa học kì Đề số 2

Câu 1:

a. Ta có:

$\begin{matrix} 2\dfrac{3}{5} + \left( {\dfrac{1}{2} + \dfrac{5}{3}} \right):\dfrac{5}{6} \hfill \\ = \dfrac{{13}}{5} + \left( {\dfrac{3}{6} + \dfrac{{10}}{6}} \right).\dfrac{6}{5} \hfill \\ = \dfrac{{13}}{5} + \dfrac{{13}}{6}.\dfrac{6}{5} \hfill \\ = \dfrac{{13}}{5} + \dfrac{{13}}{5} \hfill \\ = \dfrac{{26}}{5} \hfill \\ \end{matrix}$

b. $\left( \frac{-5}{7}+\frac{4}{9} \right):\frac{4}{5}+\left( \frac{-2}{7}+\frac{-13}{9} \right):\frac{4}{5}$

$\begin{align} & =\left( \frac{-5}{7}+\frac{4}{9}+\frac{-2}{7}+\frac{-13}{9} \right):\frac{4}{5} \\ & =\left( \frac{-5-2}{7}+\frac{4-13}{9} \right).\frac{5}{4} \\ & =\left( -1-9 \right).\frac{5}{4}=-10.\frac{5}{4}=\frac{-25}{2} \\ \end{align}$

c. Ta có:

$\begin{matrix} \dfrac{{{2^5}.{{\left( { - 49} \right)}^2}}}{{{4^5}{{.7}^3}}} = \dfrac{{{2^5}.{{\left( {{7^2}} \right)}^2}}}{{{{\left( {{2^2}} \right)}^5}{{.7}^3}}} \hfill \\ = \dfrac{{{2^5}{{.7}^4}}}{{{2^{10}}{{.7}^3}}} = \dfrac{{{7^{4 - 3}}}}{{{2^{10 - 5}}}} = \dfrac{7}{{{2^5}}} = \dfrac{7}{{32}} \hfill \\ \end{matrix}$

d. Ta có:

${{\left( \dfrac{-4}{3} \right)}^{3}}:\dfrac{{{\left( \dfrac{-1}{3} \right)}^{2}}}{6}=\dfrac{{{\left( -4 \right)}^{3}}}{{{3}^{3}}}.\dfrac{6}{\dfrac{1}{{{3}^{2}}}}$ = -64 . 6 = -384

Câu 2:

a. $\frac{3}{4}-x=\frac{3}{5}$

$\begin{align} & \Rightarrow x=\frac{3}{4}-\frac{3}{5} \\ & \Rightarrow x=\frac{3}{20} \\ \end{align}$

Vậy x = 3/20

b. $\frac{1}{4}-\left( \frac{2}{5}+2x \right)=\frac{2}{3}$

$\begin{align} & \Rightarrow \frac{2}{5}+2x=\frac{1}{4}-\frac{2}{3}=\frac{-5}{12} \\ & \Rightarrow 2x=\frac{-5}{12}-\frac{2}{5}=\frac{-49}{60} \\ & \Rightarrow x=\frac{-49}{60}:2 \\ & \Rightarrow x=\frac{-49}{120} \\ \end{align}$

Vậy x = -49/120

c. $4 - \left| {x - \frac{1}{5}} \right| = \frac{1}{3}$

$\begin{matrix} 4 - \left| {x - \dfrac{1}{5}} \right| = \dfrac{1}{3} \hfill \\ \Rightarrow \left| {x - \dfrac{1}{5}} \right| = 4 - \dfrac{1}{3} \hfill \\ \Rightarrow \left| {x - \dfrac{1}{5}} \right| = \dfrac{{11}}{3} \hfill \\ \end{matrix}$

Trường hợp 1:

$\begin{matrix} x - \dfrac{1}{5} = \dfrac{{11}}{3} \hfill \\ \Rightarrow x = \dfrac{{11}}{3} + \dfrac{1}{5} \hfill \\ \Rightarrow x = \dfrac{{58}}{{15}} \hfill \\ \end{matrix}$

Trường hợp 2:

$\begin{matrix} x - \dfrac{1}{5} = - \dfrac{{11}}{3} \hfill \\ \Rightarrow x = - \dfrac{{11}}{3} + \dfrac{1}{5} \hfill \\ \Rightarrow x = \dfrac{{ - 52}}{{15}} \hfill \\ \end{matrix}$

Vậy x = 58/15 hoặc x = -52/15

Câu 3:

Gọi chiều dài hình chữ nhật là x cm

Chiều rộng hình chữ nhật là y cm, ( điều kiện: y < x)

Chu vi hình chữ nhật bằng 60cm nên nửa chu vi hình chữ nhật là

x + y = 60 : 2 = 30 (cm)

Theo bài ra tỉ lệ hai cạnh của hình chữ nhật là 2 : 3 nghĩa là:

$\begin{matrix} \dfrac{x}{3} = \dfrac{y}{2} = \dfrac{{x + y}}{{3 + 2}} = \dfrac{{30}}{5} = 6 \hfill \\ \Rightarrow \dfrac{x}{3} = 6 \Rightarrow x = 16.3 = 48 \hfill \\ \Rightarrow \dfrac{y}{2} = 6 \Rightarrow y = 6.2 = 12 \hfill \\ \end{matrix}$

Vậy chiều dài hình chữ nhật là 48 cm

Chiều rộng hình chữ nhật là 12 cm

Câu 4:

a. Ta có:

$\widehat {{D_2}} = {135^0},\widehat {ADB} = {60^0} \Rightarrow \widehat {{D_4}} = 360 - 135 - 60 = {165^0} = \widehat {{B_2}}$

=> d // m (do 2 góc ở vị trí so le trong)

Vậy đường thẳng d sông song với đường thẳng m

b. Ta có: $\widehat {{D_1}} + \widehat {{D_2}} = {180^0} \Rightarrow \widehat {{D_1}} = 180 - 135 = {45^0}$

Do d // d’ nên $\widehat {{A_1}} = \widehat {{D_1}} = {45^0}$

Ta có:

$\widehat {{D_1}} + \widehat {{D_3}} = {60^0} \Rightarrow \widehat {{D_3}} = 60 - 45 = {15^0}$

Câu 5:

Ta có:

$\begin{matrix} \dfrac{x}{2} = \dfrac{y}{{ - 3}} = \dfrac{z}{4} \Rightarrow \frac{{2x}}{4} = \dfrac{{ - 3y}}{9} = \dfrac{z}{4} \hfill \\ \Rightarrow 2x = z, - 3y = \dfrac{{9z}}{4} \hfill \\ \Rightarrow 2x - 3y + 5z = z + \dfrac{{9z}}{4} + 5z = \dfrac{{33}}{4}z\left( * \right) \hfill \\ \end{matrix}$

Tương tự ta có:

$\begin{matrix} \dfrac{x}{2} = \dfrac{y}{{ - 3}} = \dfrac{z}{4} \Rightarrow \dfrac{{4x}}{8} = \dfrac{{5y}}{{ - 15}} = \dfrac{z}{4} \hfill \\ \Rightarrow 4x = 2z, - 5y = \dfrac{{ - 15z}}{4} \hfill \\ \Rightarrow 4x + 5y - 2z = 2z + \dfrac{{ - 15z}}{4} - 2z = \dfrac{{ - 15}}{4}z(**) \hfill \\ \end{matrix}$

Từ (*) và (**) ta có:

$A = \dfrac{{2x - 3y + 5z}}{{4x + 5y - 2z}} = \dfrac{{\dfrac{{33}}{4}z}}{{\dfrac{{ - 15}}{4}z}} = \dfrac{{ - 11}}{5}$

Mời các bạn tải tài liệu miễn phí tham khảo hướng dẫn giải chi tiết!

-------------------------------------------------

Trên đây là Giaitoan.com giới thiệu tới quý thầy cô và bạn đọc Đề kiểm tra giữa học kì 1 môn Toán lớp 7 năm học 2020 - 2021 Đề 2. Chúc các bạn học tốt và nhớ thường xuyên tương tác với GiaiToan.com để có thêm nhiều tài liệu chất lượng miễn phí nhé!