Bài 70 trang 95 SGK Toán 9 tập 2

Giải SGK Toán 9

1 Đánh giá

Toán 9 Bài 9 Độ dài đường tròn, cung tròn

Giải Toán 9 Bài 70 Trang 95 SGK Độ dài đường tròn, cung tròn với hướng dẫn và lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa môn Toán 9, các bài giải tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải Toán 9.

Bài 70 trang 95 SGK Toán 9 tập 2

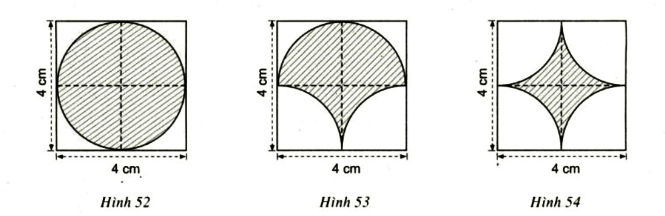
Bài 70 (SGK trang 95): Vẽ lại ba hình (tạo bởi các cung tròn) dưới đây và tính chu vi của mỗi hình (có gạch chéo)

Bài 70 trang 95 SGK Toán 9 tập 2

Hướng dẫn giải

Chu vi đường tròn $C = 2\pi R$

Công thức tính độ dài cung tròn: $l = \frac{{\pi Rn}}{{180}}$

Lời giải chi tiết

Hình 52: Phần gạch chéo là đường tròn đường kính d = 4cm

⇒ Chu vi của hình là: C = π.d = 4π ≈ 12,57 (cm)

Hình 53: Chu vi gồm nửa đường tròn C; cung tròn C₁ và cung tròn C₂

C là nửa đường tròn đường kính d = 4cm

⇒ C = π.R = 2π (cm)

C₁ và C₂ là $\frac{1}{4}$ đường tròn bán kính R = 2cm

$\Rightarrow {C_1} = {C_2} = \frac{1}{4}.2\pi .R = \frac{1}{4}.2\pi .2 = \pi$

Vậy chu vi phần gạch chéo bằng:

C + C₁ + C₂ = 2π + π + π = 4π ≈ 12,57 (cm)

- Hình 54:

Chu vi cần tính là 4 cung tròn C₁; C₂; C₃; C₄

C₁; C₂; C₃; C₄ đều là $\frac{1}{4}$ đường tròn bán kính R = 2cm.

$\Rightarrow {C_1}{\text{ = }}{C_2} = {C_3}\; = {C_4} = \frac{1}{4}.2\pi .R = \pi \left( {cm} \right)$

⇒ Chu vi phần hình gạch chéo: C = C₁ + C₂ + C₃ + C₄ = 4π ≈ 12,57 (cm).

------------------------------------------------

Trên đây GiaiToan đã chia sẻ Giải Toán 9: Độ dài đường tròn, cung tròn. Hy vọng với tài liệu này sẽ giúp ích cho các bạn học sinh tham khảo, chuẩn bị cho bài giảng sắp tới tốt hơn. Chúc các bạn học tập tốt!