Giaitoan.com Toán 10 Giải Toán 10 CTST Tập 1

Bài 6 trang 59 Toán 10 tập 1 SGK Chân trời sáng tạo Giải Toán 10 sách Chân trời sáng tạo

Nội dung
  • 1 Đánh giá

Bài 6 trang 59 SGK Toán 10

Toán lớp 10 Bài 6 trang 59 là lời giải bài Bài tập cuối chương 3 trang 59 SGK Toán 10 sách Chân trời sáng tạo hướng dẫn chi tiết lời giải giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải Toán 10. Mời các em học sinh cùng tham khảo chi tiết.

Giải bài 6 Toán 10 trang 59

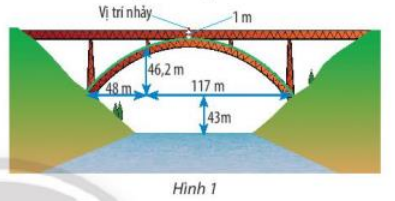
Bài 6 (SGK trang 59): Nhảy bungee là một trò chơi mạo hiểm. Trong trò chơi này, người chơi đứng ở vị trí trên cao, thắt dây an toàn vả nhảy xuống. Sợi dây này có tính đàn hồi và được tính toán chiều dài để nó kéo người chơi lại khi gần chạm đất (hoặc mặt nước).

Bài 6 trang 59 Toán 10 tập 1 SGK Chân trời sáng tạo

Chiếc cầu trong Hình 1 có bộ phận chống đỡ dạng parabol. Một người thực hiện một cú nhảy bungee từ giữa cầu xuống với dây an toàn. Người này cần trang bị sợi dây an toàn dài bao nhiêu mét? Biết rằng chiều dài của sợi dây đó bằng một phần ba khoảng cách từ vị trí bắt đầu nhảy đến mặt nước.

Lời giải chi tiết

Kí hiệu bằng hình vẽ như sau:

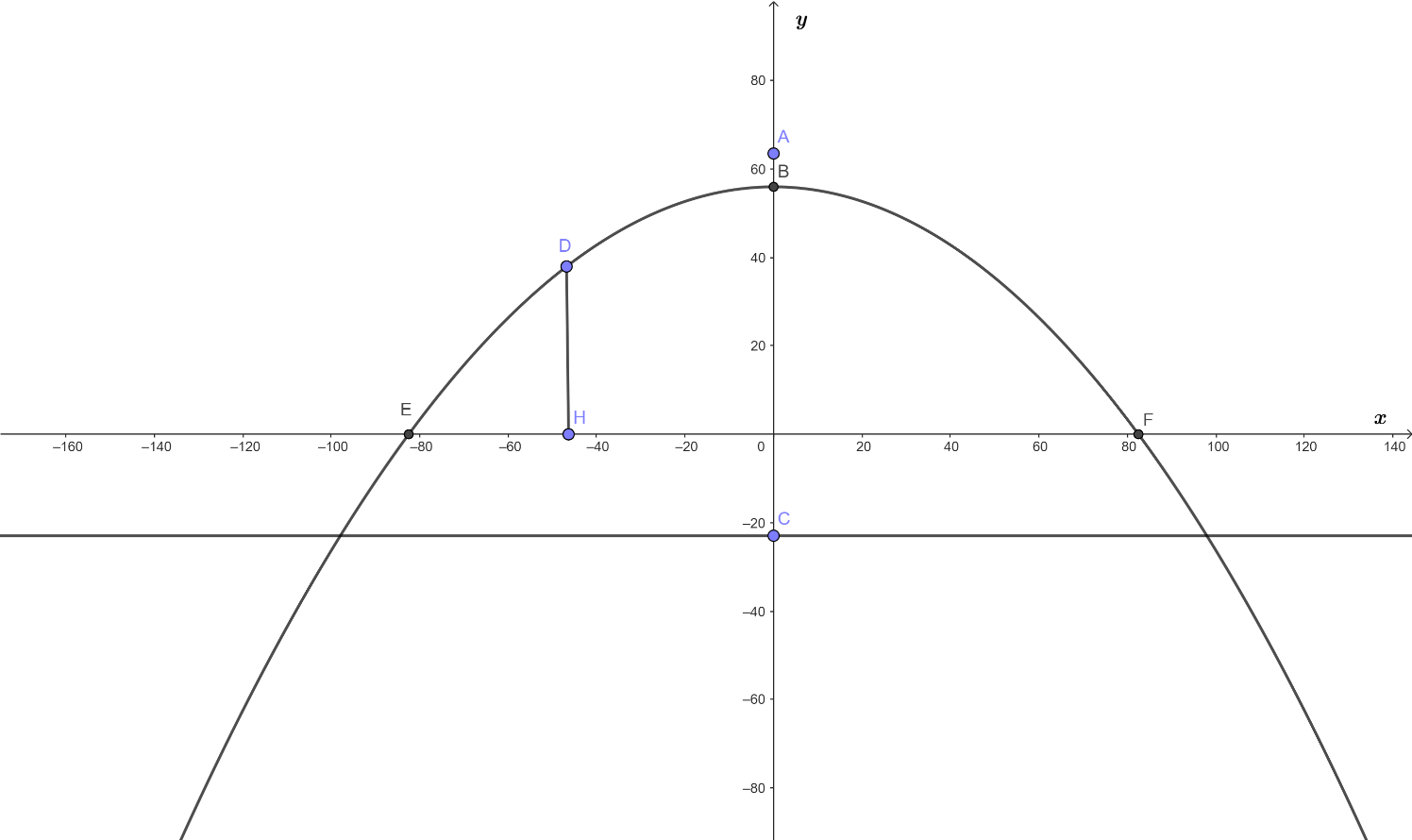
Bài 6 trang 59 Toán 10 tập 1 SGK Chân trời sáng tạo

Điểm A là vị trí nhảy, E và F là chân bộ phận chống đỡ cầu.

Theo hình vẽ ta có:

Bộ phận chống đỡ cầu có dạng parabol (P)

=> Phương trình có dạng: y = ax2 + bx + c.

EF = 48 + 117 = 165 m

OE = EF : 2 = 165 : 2 = 82,5m

=> OH = OE – EH = 34,5 m

=> Tọa độ các điểm như sau: D(34,5; 46,2), E(-82,5; 0) và F(82,5; 0).

Vì các điểm D, E, F thuộc (P) nên ta có hệ phương trình:

\begin{matrix} \left\{ {\begin{array}{*{20}{c}} {{{\left( { - 82,5} \right)}^2}a - 82,5b + c = 0} \\ \begin{gathered} {\left( {82,5} \right)^2}a + 82,5b + c = 0 \hfill \\ {\left( {34,5} \right)^2}a - 82,5b + c = 0 \hfill \\ \end{gathered} \end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}} {a = - \dfrac{{77}}{{9360}}} \\ \begin{gathered} b = 0 \hfill \\ c = \dfrac{{46565}}{{832}} \hfill \\ \end{gathered} \end{array}} \right. \hfill \\ \Rightarrow y = \dfrac{{ - 77}}{{9360}}{x^2} + \dfrac{{46565}}{{832}} \hfill \\ {x_B} = 0 \Rightarrow {y_B} = \dfrac{{ - 77}}{{9360}}.0 + \dfrac{{46565}}{{832}} = \dfrac{{46565}}{{832}} \hfill \\ \Rightarrow B\left( {0;\dfrac{{46565}}{{832}}} \right) \Rightarrow OB = \dfrac{{46565}}{{832}}\left( m \right) \hfill \\ \end{matrix}

Khoảng cách từ vị trí nhảy đến mặt nước là:

AB + OB + OC \approx 99,97\left( m \right)

Độ dài sợi dây là: 99,97: 3 = 33,32 m

-----> Câu hỏi tiếp theo: Bài 7 trang 59 SGK Toán 10

----------------------------------------

Trên đây là lời giải chi tiết Bài 6 Toán lớp 10 trang 59 Bài tập cuối chương 3 trang 59 cho các em học sinh tham khảo, nắm được cách giải các dạng toán của Chương 3: Hàm số bậc hai và đồ thị . Hi vọng đây là tài liệu hữu ích cho các bạn ôn tập kiểm tra năng lực, bổ trợ cho quá trình học tập trong chương trình THPT cũng như ôn luyện cho kì thi THPT Quốc gia. Chúc các bạn học tốt!

Chia sẻ bởi: Đội Trưởng Mỹ
Mời bạn đánh giá!
  • Lượt xem: 730
Tìm thêm: Toán 10 Giải Toán 10
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần