Bài 4 trang 82 Toán 7 tập 2 SGK Chân trời sáng tạo Giải Toán 7 Chân trời sáng tạo

Bài 4 trang 82 SGK Toán 7 tập 2

Bài 4 trang 82 Toán lớp 7 tập 2 thuộc bài 9 Tính chất ba đường phân giác của tam giác được hướng dẫn chi tiết dưới đây giúp cho các em học sinh ôn tập, củng cố kỹ năng giải Toán 7 nhằm chuẩn bị cho các bài kiểm tra đạt kết quả cao.

Giải Bài 4 Toán 7 tập 2 SGK trang 82

Bài 4 (SGK trang 82): Cho tam giác DEF. Tia phân giác của góc D và E cắt nhau tại I. Qua I kẻ đường thẳng song song với EF, đường thẳng này cắt DE tại M, cắt DF tại N. Chứng minh rằng ME + NF = MN.

Lời giải:

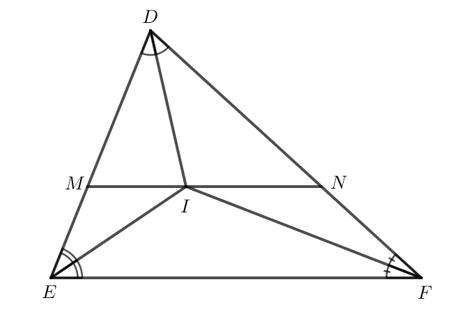
Tam giác DEF có I là giao điểm hai đường phân giác.

Mà ba đường phân giác của tam giác DEF đồng quy nên IF là đường phân giác của

EI là đường phân giác của nên

Do IM // EF nên (2 góc so le trong).

Suy ra

Tam giác MIE có  nên tam giác MIE cân tại M.

Do đó ME = MI (1).

FI là đường phân giác của nên

Do IN // EF nên  (2 góc so le trong).

Suy ra

Tam giác NIF có  nên tam giác NIF cân tại N.

Do đó NI = NF (2).

Từ (1) và (2) ta có ME + NF = MI + NI = MN.

Vậy ME + NF = MN.

Câu hỏi trong bài: Giải Toán 7 Bài 9: Tính chất ba đường phân giác của tam giác

Câu hỏi cùng bài:

• Bài 3 (SGK trang 82): Cho tam giác ABC cân tại A. Tia phân giác...
• Bài 5 (SGK trang 82): Cho tam giác AMN vuông tại A...
• Bài 6 (SGK trang 82): Ba thành phố A, B, C được nối với nhau...

Bài 4 trang 82 Toán 7 tập 2 SGK CTST được GiaiToan đăng tải lời giải chi tiết cho các em học sinh tham khảo, nắm được cách giải các dạng toán của Chương 8: Tam giác. Qua đó giúp các em học sinh ôn tập chuẩn bị cho các bài thi giữa và cuối học kì lớp 7 đạt kết quả cao. Ngoài ra Giaitoan mời thầy cô và học sinh tham khảo thêm các câu hỏi, bài tập hay bài học khác trong chuyên mục Toán 7 sách Chân trời sáng tạo.