Bài 4 trang 66 Toán 7 tập 2 SGK Chân trời sáng tạo Giải Toán 7 Chân trời sáng tạo

Bài 4 trang 66 SGK Toán 7 tập 2

Bài 4 trang 66 Toán lớp 7 tập 2 thuộc bài 4 Đường vuông góc và đường xiên được GiaiToan hướng dẫn chi tiết giúp cho các em học sinh ôn tập, củng cố kỹ năng giải Toán 7.

Giải Bài 4 Toán 7 tập 2 SGK trang 66

Bài 4 (SGK trang 66): Quan sát Hình 10.

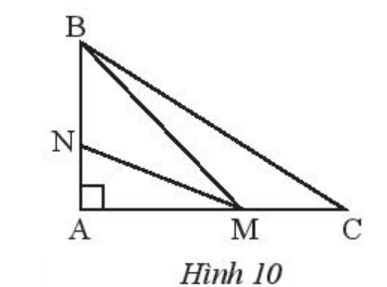
a) Tìm đoạn ngắn nhất trong các đoạn BA, BM, BC.

b) Tìm đoạn ngắn nhất trong các đoạn MA, MN, MB.

c) Chứng minh rằng MA < BC.

Lời giải:

a) Ta thấy BA là đường vuông góc kẻ từ B đến AC.

BM và BC là đường xiên kẻ từ B đến AC.

Do đó BA là đoạn ngắn nhất trong các đoạn BA, BM, BC.

b) Ta thấy MA là đường vuông góc kẻ từ M đến AB.

MN và MB là đường xiên kẻ từ M đến AB.

Do đó MA là đoạn ngắn nhất trong các đoạn MA, MN, MB.

c) Ta có MA < MB (1).

  (2 góc kề bù) nên

(tổng 3 góc trong tam giác ABM) nên

Do đó

Khi đó  là góc tù.

Tam giác BMC có là góc tù nên  là góc lớn nhất trong tam giác BMC.

Khi đó BC là cạnh lớn nhất trong tam giác BMC.

Do đó BM < BC (2).

Từ (1) và (2) ta có MA < MB < BC nên MA < BC.

Câu hỏi trong bài: Giải Toán 7 Bài 4: Đường vuông góc và đường xiên

Câu hỏi cùng bài:

• Bài 3 (SGK trang 66) : Cho tam giác ABC vuông tại A có...
• Bài 5 (SGK trang 66) : Trong Hình 11a, ta gọi độ dài đoạn thẳng AB...

Bài 4 trang 66 Toán 7 tập 2 SGK CTST được GiaiToan đăng tải lời giải chi tiết cho các em học sinh tham khảo, nắm được cách giải các dạng toán của Chương 8: Tam giác. Qua đó giúp các em học sinh ôn tập chuẩn bị cho các bài thi giữa và cuối học kì lớp 7 đạt kết quả cao. Ngoài ra Giaitoan mời thầy cô và học sinh tham khảo thêm các câu hỏi, bài tập hay bài học khác trong chuyên mục Toán 7 sách Chân trời sáng tạo.