Bài 25 trang 112 SGK Toán 9 tập 1 Giải SGK Toán 9

Bài 25 trang 112 Toán 9 Tập 1

Giải bài 25 trang 112 SGK Dấu hiệu nhận biết tiếp tuyến của đường tròn với hướng dẫn và lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa môn Toán 9, các bài giải tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán.

Bài 25 (trang 112 SGK): Cho đường tròn tâm O có bán kính OA = R, dây BC vuông góc với OA tại trung điểm M của OA.

a) Tứ giác OCAB là hình gì? Vì sao?

b) Kẻ tiếp tuyến với đường tròn tại B, nó cắt đường thẳng OA tại E. Tính độ dài BE theo R.

Hướng dẫn giải

Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.

Lời giải chi tiết

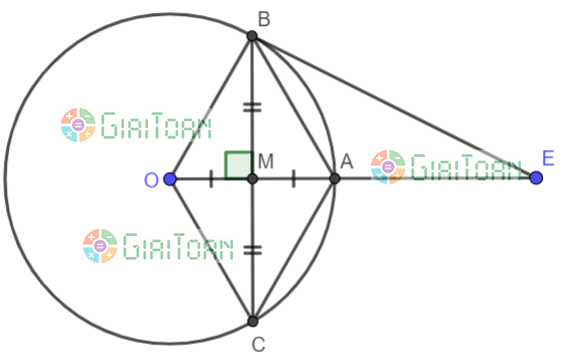
a) Bán kính OA vuông góc với BC nên MB = MC

Lại có MO = MA (giả thiết)

Suy ra tứ giác OBAC là hình bình hành vì có các đường chéo cắt nhau tại trung điểm mỗi đường.

Lại có: OA ⊥ BC nên OBAC là hình thoi.

b) Ta có: OA = OB (Bán kính)

OB = BA (Tính chất hình thoi)

=> OA = OB = BA => ΔAOB đều

$\Rightarrow \widehat {AOB} = {60^0}$

Trong tam giác OBE vuông tại B ta có:

$\Rightarrow EB = BO.\tan \widehat {AOB} = OB.\tan {60^0} = R\sqrt 3$

-----------------------------------------------------------

Trên đây GiaiToan đã chia sẻ Giải Toán 9 Bài 5 Dấu hiệu nhận biết tiếp tuyến của đường tròn giúp học sinh nắm chắc Chương 2: Đường tròn. Hy vọng với tài liệu này sẽ giúp ích cho các bạn học sinh tham khảo, chuẩn bị cho bài giảng sắp tới tốt hơn. Chúc các bạn học tập tốt!

Chia sẻ bởi: