Giaitoan.com Toán 10 Giải Toán 10 KNTT Tập 1

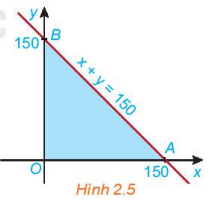
Xét biểu thức F (x; y) = 2x+ 3y với (x; y) thuộc miền tam giác OAB Giải Toán 10 sách kết nối tri thức

Nội dung
  • 1 Đánh giá

Hoạt động 3 trang 28 Toán 10 tập 1

Giải SGK Toán 10: Hoạt động 3 trang 28 Hệ bất phương trình bậc nhất hai ẩn được GiaiToan hướng dẫn giúp các học sinh luyện tập về dạng bài tính nhanh. Hi vọng tài liệu này giúp các em học sinh tự củng cố kiến thức, luyện tập và nâng cao cách giải bài tập Toán lớp 10. Mời các em cùng các thầy cô tham khảo.

Xét biểu thức F(x; y) = 2x+ 3y với (x; y) thuộc miền tam giác OAB ở HD2. Tọa độ ba đỉnh là O(0; 0), A(150; 0) và B(0; 150) (H.2.5).

Hoạt động 3 trang 28 Toán 10 tập 1 SGK Kết nối tri thức với cuộc sống

a) Tính giá trị của biểu thức F(x; y) tại mỗi đỉnh O, A và B.

b) Nêu nhận xét về dấu của hoành độ x và tung độ y của điểm (x; y) nằm trong miền tam giác OAB. Từ đó suy ra giá trị nhỏ nhất của F(x; y) trên miền tam giác OAB.

c) Nêu nhận xét về tổng x + y của điểm (x; y) nằm trong miền tam giác OAB. Từ đó suy ra giá trị lớn nhất của F(x; y) trên miền tam giác OAB.

Lời giải chi tiết

a) Tại O(0; 0)

Thay x = 0, y = 0 vào biểu thức F(x; y) = 2x + 3y, ta được:

F(0; 0) = 2.0 + 3.0 = 0

Tại A(150; 0)

Thay x = 150, y = 0 vào biểu thức F(x; y) = 2x + 3y, ta được:

F(150; 0) = 2.150 + 3.0 = 300

Tại B(0; 150)

Thay x = 0, y = 150 vào biểu thức F(x;y) = 2x + 3y, ta được:

F(0;150) = 2.0 + 3.150 = 450

b) Các điểm nằm trong miền tam giác OAB, có hoành độ x ≥ 0 và tung độ y ≥ 0.

=> F(x; y) = 2x + 3y ≥ 2.0 + 3.0 = 0

=> Giá trị nhỏ nhất của F(x; y) = 0 tại O(0; 0).

c) Các điểm nằm trong miền tam giác OAB có hoành độ x và tung độ y thỏa mãn:

0 ≤ x + y ≤ 150

=> 0 ≤ 2x + 2y ≤ 300

=> 0 ≤ 2x + 2y + y ≤ 300 + y

Mà 0 ≤ y ≤ 150 nên 300 + y ≤ 450

=> 0 ≤ 2x + 2y + y ≤ 450

=> 0 ≤ 2x + 3y ≤ 450

=> 0 ≤ F(x; y) ≤ 450

Vậy giá trị lớn nhất của hàm F(x; y) = 450 tại điểm B(0; 150)

A. Hệ bất phương trình bậc nhất hai ẩn

- Hệ bất phương trình bậc nhất hai ẩn là một hệ gồm hai hay nhiều bất phương trình bậc nhất hai ẩn.

- Cặp số (x0; y0) là nghiệm của một hệ bất phương trình bậc nhất hai ẩn khi (x0; y0) đồng thời là nghiệm của tất cả các bất phương trình trong hệ đó.

B. Giải hệ bất phương trình bậc nhất hai ẩn

- Trong mặt phẳng tọa độ, tập hợp các điểm có tọa độ là nghiệm của hệ bất phương trình bậc nhất hai ẩn là miền nghiệm của hệ bất phương trình đó.

- Miền nghiệm của hệ là giao các miền nghiệm của các bất phương trình trong hệ.

 Cách giải hệ bất phương trình bậc nhất hai ẩn.

+ Trên cùng một mặt phẳng tọa độ, xác định miền nghiệm của mỗi bất phương trình bậc nhất hai ẩn trong hệ và gạch bỏ miền còn lại.

+ Miền không bị gạch là miền nghiệm của hệ bất phương trình đã cho.

----> Bài học liên quan: Toán 10 Bài 4 Hệ bất phương trình bậc nhất hai ẩn

-------------------------------------------------

Ngoài dạng bài tập Chuyên đề Toán 10: Giải hệ bất phương trình bậc nhất hai ẩn các em học sinh có thể tham khảo thêm nhiều nội dung Hỏi đáp Toán lớp 10 được GiaiToan đăng tải. Với phiếu bài tập này sẽ giúp các em rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các em học tập tốt!

Chia sẻ bởi: Thùy Chi
Mời bạn đánh giá!
  • Lượt xem: 49
Tìm thêm: Toán 10 Giải Toán 10
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần