Bài 41 trang 128 SGK Toán 9 tập 1 Giải bài tập Toán 9

1 Đánh giá

Ôn tập chương 2 hình học 9

Giải Toán 9 bài 41 Trang 128 SGK Ôn tập chương 2 với hướng dẫn và lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa môn Toán 9, các bài giải tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải Toán hình 9.

Bài 41 trang 128 SGK Toán 9 tập 1

Bài 41 (trang 128 SGK): Cho đường tròn (O) có đường kính BC, dây AD vuông góc với BC tại H. Gọi E, F theo thứ tự là chân các đường vuông góc kẻ từ H đến AB, AC. Gọi (I), (K) theo thưu tự là các đường tròn ngoại tiếp tam giác HBE, HCF.

a. Hãy xác định vị trí tương đối của các đường tròn: (I) và (O), (K) và (O), (I) và (K).

b. Tứ giác AEHF là hình gì? Vì sao?

c. Chứng minh đẳng thức AE . AB = AF . AC.

d. Chứng minh rằng EF là tiếp tuyến chung của hai đường tròn (I) và (K).

e. Xác định vị trí của điểm H để EF có độ dài lớn nhất.

Hướng dẫn giải

- Trong một tam giác đường trung tuyến ứng với cạnh huyền và bằng một nửa cạnh huyền thì tam giác đó là tam giác vuông.

- Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền.

- Nếu một tam giác tạo bởi đường kính và một điểm bất kì nằm trên đường tròn thì tam giác đó là tam giác vuông.

Lời giải chi tiết

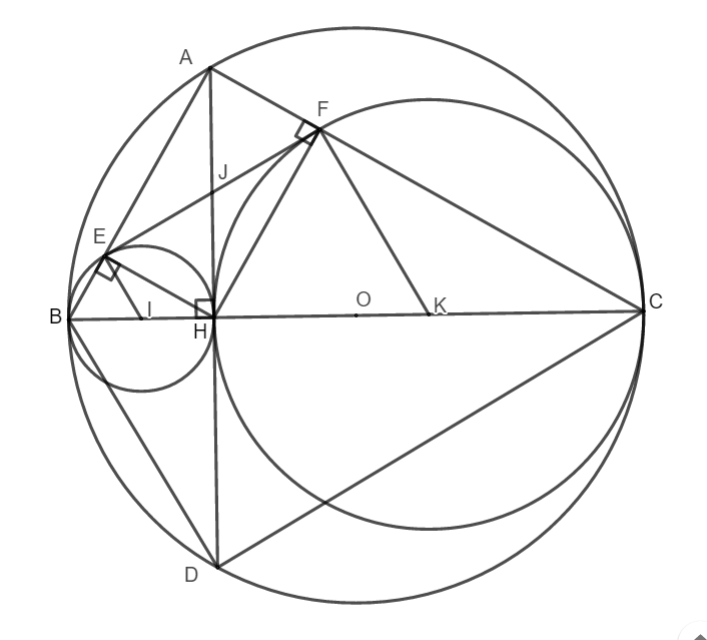
Bài 41 trang 128 SGK Toán 9 tập 1

a. Tam giác BHE vuông tại E suy ra tâm đường tròn ngoại tiếp tam giác là trung điểm của BH.

Tương tự tam giác HCF vuông tại F suy ra tâm đường trong ngoại tiếp tam giác là trung điểm của HC.

Ta có: IB < OB, điểm I nằm giữa B và O, (I) giao với (O) tại B suy ra (I) tiếp xúc trong với (O) tại B.

KC < OC, điểm K nằm giữa C và O, (K) giao với (O) tại C suy ra (I) tiếp xúc trong với (O) tại C.

(I) và (K) tiếp xúc ngoài với nhau tại H.

b. Ta có A là một điểm nằm trên đường tròn đường kính BC suy ra tam giác ABC vuông tại A

Xét tứ giác AEHF có:

$\widehat{EAF}={{90}^{0}}$

$\widehat{AFH}={{90}^{0}}$

$\widehat{AEH}={{90}^{0}}$

$\Rightarrow$ AEHF là hình chữ nhật.

c. Xét tam giác vuông ABH vuông tại H có $HE\bot AB$

Áp dụng hệ thức lượng trong tam giác vuông ta có: $A{{H}^{2}}=AE.AB$ (1)

Tương tự xét tam giác vuông ACH vuông tại H có $HF\bot AC$

Áp dụng hệ thức lượng trong tam giác vuông ta có: $A{{H}^{2}}=AF.AC$ (2)

Từ (1) và (2) $\Rightarrow AE.AB=AF.AC$

d. Gọi J là giao điểm của AH và EF.

Do AEHF là hình chữ nhật nên JA = JE = JF = JH

Xét tam giác JEI và tam giác JHI có:

JE = JH, IE = IH, IJ chung

$\Rightarrow \Delta JEI=\Delta JHI\Rightarrow \widehat{JEI}=\widehat{JHI}={{90}^{0}}$

Vậy EF là tiếp tuyến của (I)

Chứng minh tương tự EF là tiếp tuyến của (K)

Vậy EF là tiếp tuyến chung của (I) và (K)

e. Ta có: EF = AH (vì AEHF là hình chữ nhật)

$\Rightarrow EF=AH=\frac{AD}{2}$

EF có độ dài lớn nhất khi và chỉ khi AD có độ dài lớn nhất. Khi đó dây AD là đường kính.

Vậy khi AD vuông góc với BC tại O thì EF có độ dài lớn nhất.

-----------------------------------------------------------

Trên đây GiaiToan đã chia sẻ Giải Toán hình 9: Ôn tập chương 2. Hy vọng với tài liệu này sẽ giúp ích cho các bạn học sinh tham khảo, chuẩn bị cho bài giảng sắp tới tốt hơn. Chúc các bạn học tập tốt!