Bài 42 trang 128 SGK Toán 9 tập 1 Giải bài tập Toán 9

1 Đánh giá

Ôn tập chương 2 hình học 9

Giải Toán 9 bài 42 Trang 128 SGK Ôn tập chương 2 với hướng dẫn và lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa môn Toán 9, các bài giải tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải Toán hình 9.

Bài 42 trang 128 SGK Toán 9 tập 1

Bài 42 (trang 128 SGK): Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A, BC là tiếp tuyến chung ngoài, . Tiếp tuyến chung trong tại A cắt BC ở điểm M. Gọi E là giao điểm củ OM và AB, F là giao điểm của O’M và AC. Chứng minh rằng:

a. Tứ giác AEMF là hình chữ nhật.

b. ME . MO = MF . MO’

c. OO’ là tiếp tuyến của đường tròn có đường kính là BC.

d. BC là tiếp tuyến của đường tròn có đường kính OO’.

Hướng dẫn giải

* Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì:

- Điểm đó cách đều hai điểm.

- Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.

- Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.

* Trong một tam giác đường trung tuyến bằng một nửa cạnh huyền thì tam giác đó là tam giác vuông.

Lời giải chi tiết

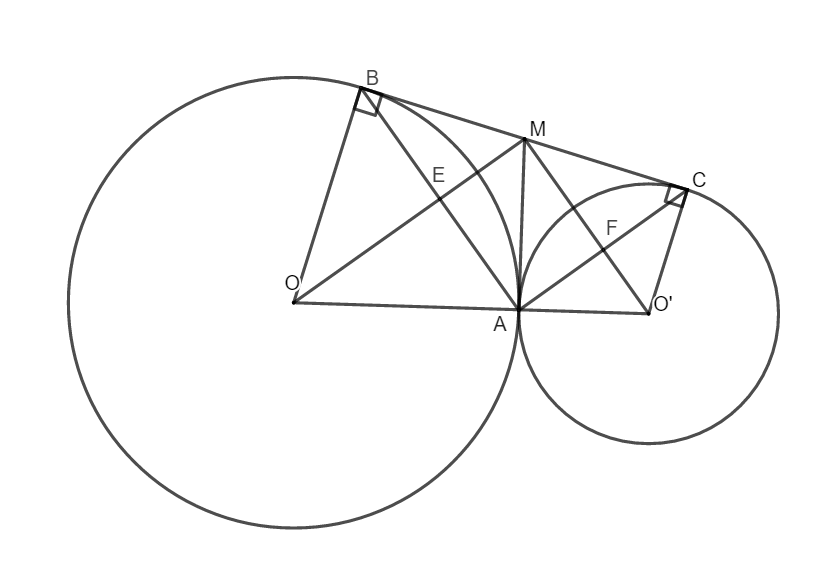
Bài 42 trang 128 SGK Toán 9 tập 1

a. Ta có: MB, MA là tiếp tuyến của đường tròn (O) nên MA = MB (tính chất hai tiếp tuyến cắt nhau) (1)

Ta lại có MA, MC là tiếp tuyến của đường tròn (O’) nên MA = MC (tính chất hai tiếp tuyến cắt nhau) (2)

Từ (1) và (2) suy ra MA = MB = MC

Xét tam giác ABC có MA là tiếp tuyến và vuông tại A

$\Rightarrow \widehat{BAC}={{90}^{0}}$

Xét tam giác MBA cân tại M có EM là phân giác nên ME cũng là đường cao $\Rightarrow ME\bot AB\Rightarrow \widehat{AEM}={{90}^{0}}$

Xét tam giác MCA cân tại M có FM là phân giác nên MF cũng là đường cao $\Rightarrow MF\bot AC\Rightarrow \widehat{AFM}={{90}^{0}}$

Xét tứ giác AEMF có

$\widehat{BAC}={{90}^{0}}$

$\widehat{AFM}={{90}^{0}}$

$\widehat{AEM}={{90}^{0}}$

$\Rightarrow AEMF$ là hình chữ nhật.

b. Xét tam giác AOM vuông tại A có $AE\bot MO$

Áp dụng hệ thức lượng trong tam giác ta có: $M{{A}^{2}}=ME.MO$ (3)

Tương tự Xét tam giác AO’M vuông tại A có $AF\bot MO'$

Áp dụng hệ thức lượng trong tam giác ta có: $M{{A}^{2}}=MF.MO'$ (4)

Từ (3) và (4) $\Rightarrow ME.MO=MF.MO'$

c. Ta có MA = MB = MC (chứng minh câu a) $\Rightarrow$ A, B, C nằm trên đường tròn tâm M bán kính MA

Mặt khác $OO'\bot MA$ tại A

$\Rightarrow$ OO’ là tiếp tuyến của đường tròn tâm M đường kính BC.

d. Ta có: $\left\{ \begin{matrix} OB\bot BC \\ OC\bot BC \\ \end{matrix}\Rightarrow OB//OC \right.\Rightarrow OBCO'$ là hình thang.

Gọi I là trung điểm của OO’. Ta có M là trung điểm của BC

$\Rightarrow$ MI là đường trung bình của hình thang OBCO’

$\Rightarrow$ MI // OB // OC’ mà $\left\{ \begin{matrix} OB\bot BC \\ OC\bot BC \\ \end{matrix}\Rightarrow \right.MI\bot BC$ (5)

Ta có: AEMF là hình chữ nhật $\Rightarrow \widehat{OMO'}={{90}^{0}}\Rightarrow \Delta OMO'$ vuông tại M

Ta lại có MI là trung tuyến của tam giác OMO’ nên MI = IO = IO’

$\Rightarrow$ O, M, O’ nằm trên đường tròn tâm I đường kính OO’ (6)

Từ (5) và (6) ta suy ra BC là tiếp tuyến của đường tròn tâm I đường kính OO’.

-----------------------------------------------------------

Trên đây GiaiToan đã chia sẻ Giải Toán hình 9: Ôn tập chương 2. Hy vọng với tài liệu này sẽ giúp ích cho các bạn học sinh tham khảo, chuẩn bị cho bài giảng sắp tới tốt hơn. Chúc các bạn học tập tốt!