Giaitoan.com Toán 7 Luyện tập Toán 7 CD

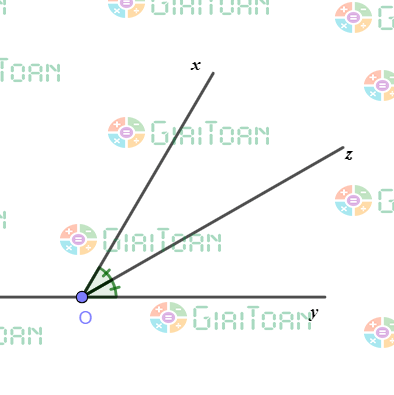
Luyện tập Góc ở vị trí đặc biệt. Tia phân giác của một góc Sách Cánh Diều Bài tập Toán 7 Sách Cánh Diều

Nội dung
  • 4 Đánh giá

Bài tập Toán 7 Góc ở vị trí đặc biệt. Tia phân giác của một góc - Có đáp án

GiaiToan.com xin giới thiệu đến bạn đọc tài liệu Bài test: Trắc nghiệm Góc ở vị trí đặc biệt. Tia phân giác của một góc được xây dựng dựa trên kiến thức trọng tâm sách Cánh Diều. Nhằm giúp học sinh củng cố và rèn luyện kỹ năng tính toán, khả năng tư duy với các dạng bài tập Toán lớp 7 mới nhất. Tham gia làm bài test để làm quen với các dạng toán Chương 4: Góc vè đường thẳng song song

Bài tập Toán 7 Sách Cánh Diều có đáp án được trình bày dưới dạng bài tập trực tuyến nên các em học sinh có thể trực tiếp vào làm bài và kiểm tra kết quả ngay khi làm xong. Bài tập có đáp án và hướng dẫn giải chi tiết giúp các em hiểu cách làm bài hơn.

Ngoài ra mời thầy cô và học sinh tham khảo thêm một số tài liệu liên quan: Luyện tập Toán lớp 7, Đề thi học kì 1 lớp 7 Có đáp án chi tiết, ...

------> Bài tiếp theo: Luyện tập Hai đường thẳng song song

------> Bài liên quan:

Bạn đã dùng hết 5 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản Giaitoan PRO để tiếp tục! Tìm hiểu thêm
Giaitoan PRO chỉ từ 79.000đ
Bạn đã mua gói? Đăng nhập ngay!
  • Câu 1:

    Cho hình vẽ sau.

    Luyện tập Góc ở vị trí đặc biệt. Tia phân giác của một góc Sách Cánh Diều

    Chọn khẳng định đúng:

    Gợi ý lời giải:

    Quan sát hình vẽ ta thấy:

    Tia Oz nằm giữa hai tia Ox, Oy

    Số đo góc xOz bằng số đo góc zOt

    Vậy Oz là tia phân giác góc xOy

  • Câu 2:

    Trong hình vẽ dưới đây:

    Luyện tập Góc ở vị trí đặc biệt. Tia phân giác của một góc Sách Cánh Diều

    Góc nào là góc kề bù với góc QOS?

    Gợi ý lời giải:

    - Hai góc có một cạnh chung, hai cạnh còn lại là hai tia đối nhau được gọi là hai góc kề bù.

    - Hai góc kề bù có số đo bằng 1800.

    Vậy góc SOP là góc kề bù của góc QOS.

  • Câu 3:

    Cho hình vẽ dưới đây:

    Luyện tập Góc ở vị trí đặc biệt. Tia phân giác của một góc Sách Cánh Diều

    Biết góc AOD bằng 3100. Tính số đo góc COD.

    Gợi ý lời giải:

    Hai đường thẳng AC và BD cắt nhau tại O tạo thành bốn góc có tổng số đo bằng 3600

    => \widehat {AOB} + \widehat {BOC} + \widehat {COD} + \widehat {DOA} = {360^0}

    => \widehat {DOA} = {360^0} - \left( {\widehat {AOB} + \widehat {BOC} + \widehat {COD}} \right) = {360^0} - {310^0} = {50^0}

    Mặt khác \widehat {COD},\widehat {DOA} là hai góc kề bù

    \widehat {COD} + \widehat {DOA} = {180^0} \Rightarrow \widehat {COD} = {180^0} - \widehat {DOA} = {180^0} - {50^0} = {130^0}

  • Câu 4:

    Cho góc \widehat {MON} = {60^0}. Vẽ tia OA nằm giữa hai tia OM và ON sao cho OA là tia phân giác góc MON. Ta có:

    Gợi ý lời giải:

    Ta có OA là tia phân giác góc MON

    => \widehat {MOA} = \widehat {AON} = \frac{{\widehat {MON}}}{2} = {30^0}

  • Câu 5: Biết hai góc A và góc B là hai góc kề bù. Số đo góc A bằng 3 lần số đo góc B. Số đo góc B bằng bao nhiêu?
    Gợi ý lời giải:

    Ta có:

    Góc A và góc B là hai góc kề bù nên \widehat A + \widehat B = {180^0}

    Mà góc A bằng 3 lần góc B suy ra \widehat A = 3\widehat B

    \begin{matrix} 3\widehat B + \widehat B = {180^0} \hfill \\ \Rightarrow \left( {3 + 1} \right)\widehat B = {180^0} \hfill \\ \Rightarrow 4\widehat B = {180^0} \hfill \\ \Rightarrow \widehat B = {180^0}:4 = {45^0} \hfill \\ \end{matrix}

  • Câu 6:

    Cho hình vẽ:

    Luyện tập Góc ở vị trí đặc biệt. Tia phân giác của một góc Sách Cánh Diều

    Cặp góc đối đỉnh là:

    Gợi ý lời giải:

    Ta có:

    Vì hai tia OA và OC là hai tia đối nhau, hai tia OB và OD là hai tia đối nhau.

    => Cặp góc đối đỉnh là: \widehat {AOB},\widehat {COD}

  • Câu 7:

    Cho hai đường thẳng AC và BD cắt nhau tại điểm O tạo thành bốn góc khác góc bẹt. Biết \widehat {AO}C = 5\widehat {BOC}. Số đo góc AOD là bao nhiêu?

    Gợi ý lời giải:

    Luyện tập Góc ở vị trí đặc biệt. Tia phân giác của một góc

    Ta có: Góc AOC là góc bẹt

    => \widehat {AO}C = {180^0}

    Mà \widehat {AOC} = 5\widehat {BOC} \Rightarrow \widehat {BOC} = \frac{{\widehat {AOC}}}{5} = {36^0}

    Mặt khác \widehat {BOC},\widehat {AOD} là hai góc đối đỉnh

    \Rightarrow \widehat {BOC} = \widehat {AOD} = {36^0}

  • Câu 8:

    Cho góc AOB có số đo là 1400. Vẽ tia phân giác OC của góc đó, vẽ tia phân giác OD của góc BOC. Số đo góc DOA bằng bao nhiêu?

    Gợi ý lời giải:

    Luyện tập Góc ở vị trí đặc biệt. Tia phân giác của một góc Sách Cánh Diều

    Ta có: OC là tia phân giác góc BOA

    => \widehat {AOC} = \widehat {COB} = \frac{{\widehat {AOB}}}{2} = \frac{{{{140}^0}}}{2} = {70^0}

    Ta lại có: OD là tia phân giác góc BOC

    => \widehat {DOC} = \widehat {DOB} = \frac{{\widehat {COB}}}{2} = \frac{{{{70}^0}}}{2} = {35^0}

    => \widehat {DOA} = \widehat {DOC} + \widehat {COA} = {35^0} + {70^0} = {105^0}

  • Câu 9: Cho sáu tia chung gốc OA, OB, OC, OD, OE, OF trong đó OA, OB là hai tia đối nhau. Hỏi có bao nhiêu cặp góc kề bù?
    Gợi ý lời giải:
    Luyện tập Góc ở vị trí đặc biệt. Tia phân giác của một góc Sách Cánh Diều
  • Câu 10: Có n đường thẳng cắt nhau tại một điểm. Hỏi có bao nhiêu cặp góc đối đỉnh được tạo thành (không tính góc bẹt)?
    Gợi ý lời giải:

    Với n đường thẳng cắt nhau tại một điểm ta được 2n tia chung gốc.

    Chọn 1 tia trong 2n tia chung gốc đã cho tạo thành 2n – 1 tia còn lại, ta được 2n – 1 (góc)

    Tương tự như vậy với 2n tia chung gốc, ta được 2n(2n – 1) (góc)

    Nhưng vì mỗi góc đã cho được tình hai lần nên số góc thực tế là \frac{{2n\left( {2n - 1} \right)}}{2} = n\left( {2n - 1} \right) (góc)

    Vì có n đường thẳng nên sẽ có n góc bẹt.

    => Số góc khác góc bẹt là n(2n – 1) – n = n(2n – 2)

    Mỗi góc trong số n(2n – 2) đều có một góc đối đỉnh với nó

    Suy ra số cặp góc đối đỉnh là \frac{{n\left( {2n - 2} \right)}}{2} = n\left( {n - 1} \right)

  • Đáp án đúng của hệ thống
  • Trả lời đúng của bạn
  • Trả lời sai của bạn
Bắt đầu ngay
Bạn còn 5 lượt làm bài tập miễn phí. Hãy mua tài khoản Giaitoan PRO để học không giới hạn nhé! Bạn đã dùng hết 5 lượt làm bài tập miễn phí! Hãy mua tài khoản Giaitoan PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé! Mua ngay
Kiểm tra kết quả Xem đáp án Làm lại
Chia sẻ bởi: Bơ
Mời bạn đánh giá!
Tìm thêm: Toán 7 Bài tập Toán 7
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần