Giaitoan.com Toán 8 Toán 8 Kết nối tri thức

Bài 9.9 Trang 90 Toán 8 Tập 2 Kết nối tri thức Bài 34: Ba trường hợp đồng dạng của hai tam giác

Nội dung
  • 1 Đánh giá

Bài 9.9 Trang 90 Toán 8 KNTT Tập 2

Bài 9.9 Trang 90 Toán 8 KNTT là lời giải chi tiết trong bài Bài 34: Ba trường hợp đồng dạng của hai tam giác SGK Toán 8 Kết nối tri thức giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải Toán 8. Mời các em học sinh cùng tham khảo chi tiết.

Giải Bài 9.9 Trang 90 Toán 8 KNTT

Bài 9.9 (sgk trang 90): Cho góc BAC và các điểm M, N lần lượt trên các đoạn thẳng AB, AC sao cho \widehat{ABN}=\widehat{ACM}

a) Chứng minh rằng ΔABN ∽ ΔACM

b) Gọi I là giao điểm của BN và CM. Chứng minh rằng IB . IN = IC . IM

Hướng dẫn:

Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.

Lời giải chi tiết:

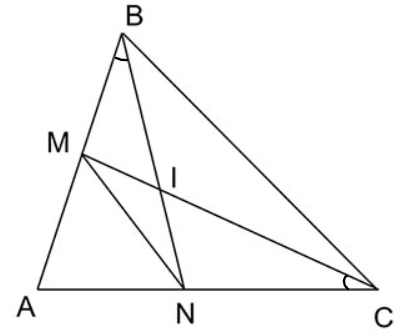
a) Xét tam giác ABN và tam giác ACM có:

Góc A chung

\widehat{ABN}=\widehat{ACM}

Vậy ΔABN ∽ ΔACM (g.g)

b) Xét tam giác IBM và tam giác ICN có:

\widehat{BIM}=\widehat{CIN} (hai góc đối đỉnh)

\widehat{IBM}=\widehat{ICN} (gt)

Vậy ΔIBM ∽ ΔICN (g.g)

Suy ra \frac{IB}{IC}=\frac{IM}{IN}=> IB . IN = IC . IM (đpcm).

---> Câu hỏi cùng bài:

---> Bài tiếp theo: Toán 8 Kết nối tri thức Bài: Luyện tập chung - Trang 91

----------------------------------------

Trên đây là lời giải chi tiết Bài 9.9 Trang 90 Toán 8 KNTT nằm trong bài Bài 34: Ba trường hợp đồng dạng của hai tam giác và ứng dụng cho các em học sinh tham khảo, nắm được cách giải các dạng bài tập của Chương 9. Qua đó giúp các em học sinh ôn tập chuẩn bị cho các bài thi giữa và cuối học kì lớp 8. Ngoài ra Giaitoan mời thầy cô và học sinh tham khảo thêm một số tài liệu liên quan: Đề thi giữa học kì 2 Toán 8, Đề thi học kì 2 Toán 8,.... Chúc các em học tốt.

Chia sẻ bởi: Bờm
Mời bạn đánh giá!
  • Lượt xem: 47
Tìm thêm: Toán 8 Toán 8 Kết nối tri thức
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần