Bài 30 trang 114 SGK Toán 8 tập 2

Giải SGK Toán 8

1 Đánh giá

Toán 8 Bài 6 Thể tích của hình lăng trụ đứng

Bài 30 Trang 114 SGK Toán 8 tập 2 biên soạn và đăng tải với hướng dẫn chi tiết lời giải giúp cho các em học sinh tham khảo, ôn tập, củng cố kỹ năng giải Toán 8. Mời các em học sinh cùng tham khảo chi tiết.

Bài 30 Trang 114 SGK Toán 8 - Tập 2

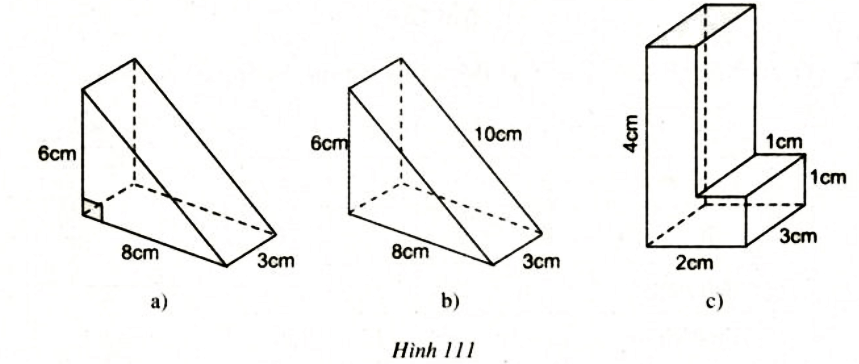
Bài 30 (SGK trang 114): Các hình a, b, c (h.111) gồm một hoặc nhiều lăng trụ đứng. Hãy tính thể tích và diện tích toàn phần của chúng theo các kích thước đã cho trên hình.

Bài 30 Trang 114 SGK Toán 8 tập 2

Hướng dẫn giải

- Thể tích hình lăng trụ đứng bằng tích chiều cao nhân diện tích đáy.

- Diện tích toàn phần bằng diện tích xung quanh cộng diện tích đáy.

Lời giải chi tiết

a. Đây là hình lăng trụ đáy là tam giác vuông chiều cao bằng 3cm

Bài 30 Trang 114 SGK Toán 8 tập 2

Tam giác GCD vuông tại C, áp dụng định lí Pi – ta – go ta có:

$C{G^2} + C{D^2} = G{D^2} \Rightarrow GD = \sqrt {C{G^2} + C{D^2}} = \sqrt {{6^2} + {8^2}} = 10\left( {cm} \right)$

Diện tích toàn phần của hình lăng trụ là:

$\begin{matrix} {S_{tp}} = 2.{S_{GCD}} + {S_{GHCF}} + {S_{GHDE}} + {S_{CFDE}} \hfill \\ \Rightarrow {S_{tp}} = 2.\frac{1}{2}.6.8 + 6.3 + 10.3 + 8.3 = 120\left( {c{m^2}} \right) \hfill \\ \end{matrix}$

Thể tích hình lăng trụ là: $V = DE.{S_{GCD}} = 3.\frac{1}{2}8.6 = 72\left( {c{m^3}} \right)$

b. Đây là hình lăng trụ đáy là tam giác chiều cao bằng 3cm.

Bài 30 Trang 114 SGK Toán 8 tập 2

Xét tam giác CGD có $C{G^2} + C{D^2} = {8^2} + {6^2} = {10^2} = G{D^2}$

Vậy tam giác GCD là tam giác vuông

Bài toán đưa về tính diện tích và thể tích giống của câu a.

Diện tích toàn phần của hình lăng trụ là:

Thể tích hình lăng trụ là: $V = DE.{S_{GCD}} = 3.\frac{1}{2}8.6 = 72\left( {c{m^3}} \right)$

Bài 30 Trang 114 SGK Toán 8 tập 2

Chia hình c thành hai lăng trụ đứng như hình vẽ:

+ Hình lăng trụ 1 là hình hộp chữ nhật có các kích thước 4, 1, 3

+ Hình lăng trụ 2 là hình hộp chữ nhật có kích thước 1, 1, 3

Diện tích toàn phần của hình 1 là: ${S_{tp1}} = {S_{xq}} + 2{S_d} = 2\left( {3 + 1} \right).4 + 2.3.1 = 38\left( {c{m^2}} \right)$

Diện tích toàn phần của hình 2 là: ${S_{tp2}} = {S_{xq}} + 2{S_d} = 2\left( {1 + 3} \right).1 + 2.3.1 = 14\left( {c{m^2}} \right)$

Diện tích toàn phần của hình lăng trụ đã cho bằng diện tích toàn phần của hai hình lăng trụ nhỏ trừ 2 lần diện tích hình chữ nhật tiếp xúc của hai lăng trụ:

${S_{tp}} = {S_{tp1}} + {S_{tp2}} - 2S = 38 + 14 - 2.3.1 = 46\left( {c{m^2}} \right)$

Thể tích hình lăng trụ 1 là: ${V_1} = 4.3.1 = 12\left( {c{m^3}} \right)$

Thể tích hình lăng trụ 2 là: ${V_2} = 1.3.1 = 3\left( {c{m^3}} \right)$

Thể tích hình lăng trụ là: $V = {V_1} + {V_2} = 12 + 3 = 15\left( {c{m^3}} \right)$

_{------------------------------------------------------------}

Trên đây là lời giải chi tiết bài tập Toán 8 Thể tích của hình lăng trụ đứng cho các em học sinh tham khảo, nắm được cách giải các dạng toán Chương 4: Hình lăng trụ đứng, Hình chóp đều Toán 8 Tập 2. Với lời giải hướng dẫn chi tiết các bạn có thể so sánh kết quả của mình từ đó nắm chắc kiến thức Toán lớp 8. Chúc các bạn học tốt và nhớ thường xuyên tương tác với GiaiToan để có thêm nhiều tài liệu chất lượng miễn phí nhé!