Giaitoan.com Toán 9 Giải Toán 9 tập 2

Bài 28 trang 120 SGK Toán 9 tập 2 Giải SGK Toán 9

Nội dung
  • 1 Đánh giá

Bài 28 trang 120 SGK Toán 9

Bài 28 trang 120 SGK Toán 9 tập 2 Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán 9. Tài liệu được biên soạn và đăng tải với hướng dẫn chi tiết các bài tập tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán. Chúc các bạn học tập tốt!

Giải bài 28 Toán 9 trang 120

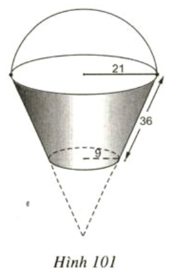
Bài 28 (trang 120 SGK): Một cái xô bằng inốc có dạng hình nón cụt đựng hóa chất, có các kích thước cho ở hình 101 (đơn vị: cm)

Bài 28 trang 120 SGK Toán 9 tập 2

a) Hãy tính diện tích xung quanh của xô.

b) Khi xô chứa đầy hóa chất thì dung tích của nó là bao nhiêu?

Hướng dẫn giải

Hình trụ

- Diện tích xung quanh hình trụ là Sxq = 2πrh

- Diện tích toàn phần hình trụ là: Stp = Sxq + 2.Sđ = 2πrh + 2πr2

- Thể tích hình trụ là: V = S.h = πr2h

Hình nón

- Diện tích xung quanh của hình nón là: Sxq = πrl

- Diện tích toàn phần của hình nón (tổng diện tích xung quanh và diện tích đáy) là: Stp = Sxq + Sđ = πrl + πr2

- Thể tích hình nón: V = \frac{1}{3}\pi {r^2}h

Lời giải chi tiết

Gọi l là đường sinh của hình nón lớn

Theo định lí Ta-lét ta có: \frac{l}{{l - 36}} = \frac{{21}}{9} \Rightarrow l = 63\left( {cm} \right)

a) Diện tích cần tính gồm diện tích xung quanh của hình xung quanh của hình nón cụt và diện tích hình tròn đáy có bán kính r = 9cm

Đường sinh của hình nón lớn là l = 63cm

Đường sinh của hình nón nhỏ là: l’ = 63 - 36 = 27 (cm)

Bán kính đáy của hình nón lớn là: R = 21cm

Diện tích xung quanh của hình nón lớn là:

{S_{xq1}} = \pi .R.l = \pi .21.63 \approx 4154,22\left( {c{m^2}} \right)

Diện tích xung quanh của hình nón nhỏ là:

{S_{xq2}} = \pi .r.l' = \pi .9.27 \approx 763,02\left( {c{m^2}} \right)

Diện tích xung quanh của xô chính là diện tích xung quanh của hình nón cụt:

{S_{xq}} = {S_{xq1}} - {S_{xq2}} = 4154,22 - 763,02 = 3391,2\left( {c{m^2}} \right)

b) Chiều cao của hình nón lớn là h ta có:

\begin{matrix} {R^2} + {h^2} = {l^2} \Rightarrow {h^2} = {l^2} - {R^2} \hfill \\ \Rightarrow h = \sqrt {{l^2} - {R^2}} = \sqrt {{{63}^2} - {{21}^2}} \approx 59,397\left( {cm} \right) \hfill \\ \end{matrix}

Chiều cao của hình nón nhỏ là h’ ta có:

\begin{matrix} {r^2} + h{'^2} = l{'^2} \Rightarrow h{'^2} = l{'^2} - {r^2} \hfill \\ \Rightarrow h' = \sqrt {{l^2} - r{'^2}} = \sqrt {{{27}^2} - {9^2}} \approx 25,456\left( {cm} \right) \hfill \\ \end{matrix}

Thể tích của hình nón lớn là:

V = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi {.21^2}.59,397 \approx 27416,467\left( {c{m^3}} \right)

Thể tích của hình nón nhỏ là:

V = \frac{1}{3}\pi {r^2}h' = \frac{1}{3}\pi {.9^2}.25,456 \approx 2158,160\left( {c{m^3}} \right)

Khi xô chứa đầy hóa chất thì dung tích của nó là thể tích của hình nón cụt là:

{V_x} = V - V' = 27416,467 - 2158,160 = 25258,307\left( {c{m^3}} \right)

----> Câu hỏi tiếp theo: Bài 29 trang 120 SGK Toán 9

-----------------------------------------------------

Trên đây là lời giải chi tiết Bài 28 trang 120 SGK Toán 9 tập 2 cho các em học sinh tham khảo, nắm được cách giải các dạng toán của Chương 4 Hình trụ - Hình nón - Hình cầu. Với lời giải hướng dẫn chi tiết các bạn có thể so sánh kết quả của mình từ đó nắm chắc kiến thức Toán lớp 9. Chúc các bạn học tốt và nhớ thường xuyên tương tác với GiaiToan để có thêm nhiều tài liệu chất lượng miễn phí nhé!

Chia sẻ bởi: Bon
Mời bạn đánh giá!
  • Lượt xem: 112
Tìm thêm: Toán 9 Giải Toán 9
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan

    Mới nhất trong tuần