Giaitoan.com Toán 9 Đề thi giữa kì 1 Toán 9

Đề thi giữa kì 1 môn Toán lớp 9 - Đề số 4 Đề kiểm tra giữa kì 1 Toán 9

Nội dung
  • 1 Đánh giá

Đề thi giữa kì 1 Toán 9 - Đề số 4

Đề thi giữa kì 1 Toán 9 - Đề số 4 được Giaitoan.com biên soạn bao gồm các dạng bài tập và đáp án chi tiết được xây dựng theo trọng tâm chương trình học THCS giúp học sinh ôn tập, củng cố kiến thức, giúp định vị khả năng tư duy logic, khả năng nhận biết. Đây là nền tảng vững chắc giúp các bạn tự tin làm bài trong các kì thi và kiểm tra định kì môn Toán 9. Mời các bạn cùng tham khảo chi tiết!

A. Đề thi Toán giữa kì 1 lớp 9

Câu 1: Thực hiện phép tính

\begin{array}{l} a)\,\,\left( {3\sqrt 8 + \sqrt {18} + 5\sqrt {\dfrac{1}{2}} - \sqrt {50} } \right).3\sqrt 2 \\ b)\,\dfrac{1}{{2 - \sqrt 3 }} + \dfrac{{\sqrt 6 - \sqrt 2 }}{{\sqrt 3 - 1}} + \sqrt {5 - 2\sqrt 6 } \\ c)\,\,\,\left( {2 + \sqrt 3 } \right)\sqrt {{{\left( {\sqrt 3 - 2} \right)}^2}} \end{array}

Câu 2: Giải phương trình

\begin{array}{l}a)\,\sqrt {4x - 8} + \dfrac{1}{2}\sqrt {16x - 32} + \sqrt {9x - 18} = 21\\b)\,\,5 - \sqrt {2x + 5} = 3\end{array}

Câu 3: Cho hai biểu thức M = \dfrac{{\sqrt x }}{{\sqrt x - 2}} + \dfrac{{\sqrt x }}{{\sqrt x + 2}} - \dfrac{{x - 2\sqrt x }}{{x - 4}} và N = \dfrac{{\sqrt x + 2}}{{\sqrt x - 2}}  ( với x \ge 0;\,\,\,x \ne 4 )

a) Tính giá trị của N biết x = 16

b) Rút gọn M

c) Cho . Tìm các giá trị nguyên của x để A < \dfrac{1}{2}

Câu 4: Để đo chiều rộng AB của một khúc sông mà không đo trực tiếp được, một người đi tuwg A đến C đo được AC = 50m và từ C nhìn thấy B với một góc nghiêng với bờ sông. Tính chiều rộng AB của khúc sông

Câu 5: Cho tam giác ABC vuông tại A có đường cao AD. Gọi AM là tia phân giác của  \widehat {DAB}

a) Tính AD; AC biết DB = 18 cm; DC = 8 cm

b) Chứng minh tam giác AMC cân tại C và

c) Gọi E, F lần lượt là hình chiếu của D lên AB và AC. Chứng minh rằng {S_{AEF}} = {S_{ABC}}\left( {1 - {{\cos }^2}B} \right).{\sin ^2}C

Câu 6: Cho 3 số dươn x, y, z . Chứng minh rằng: \dfrac{{{x^3}}}{y} + \dfrac{{{y^3}}}{z} + \,\,\dfrac{{{z^3}}}{x} \ge x\sqrt {xz} + \,\,y\sqrt {xy} + z\sqrt {yz}

B.Đáp án Đề thi giữa kì 1 lớp 9 môn Toán

Câu 1: Thực hiện phép tính:

\begin{array}{l} a)\,\,\left( {3\sqrt 8 + \sqrt {18} + 5\sqrt {\dfrac{1}{2}} - \sqrt {50} } \right).3\sqrt 2 \\ b)\,\dfrac{1}{{2 - \sqrt 3 }} + \dfrac{{\sqrt 6 - \sqrt 2 }}{{\sqrt 3 - 1}} + \sqrt {5 - 2\sqrt 6 } \\ c)\,\,\,\left( {2 + \sqrt 3 } \right)\sqrt {{{\left( {\sqrt 3 - 2} \right)}^2}} \end{array}

Hướng dẫn giải

\begin{array}{l} a)\,\,\left( {3\sqrt 8 + \sqrt {18} - \sqrt {50} } \right).\dfrac{{\sqrt 2 }}{2}\\ = \left( {6\sqrt 2 + 3\sqrt 2 - 5\sqrt 2 } \right).\dfrac{{\sqrt 2 }}{2}\\ = 4\sqrt 2 .\dfrac{{\sqrt 2 }}{2} = 4\\ b)\,\dfrac{1}{{2 - \sqrt 3 }} + \dfrac{{\sqrt 6 - \sqrt 2 }}{{\sqrt 3 - 1}} + \sqrt {5 - 2\sqrt 6 } \\ = \dfrac{{\left( {2 + \sqrt 3 } \right)}}{{\left( {2 - \sqrt 3 } \right)\left( {2 + \sqrt 3 } \right)}} + \dfrac{{\sqrt 2 \left( {\sqrt 3 - 1} \right)}}{{\sqrt 3 - 1}} + \sqrt {3 - 2\sqrt 2 .\sqrt 3 + 2} \\ = 2 + \sqrt 3 + \sqrt 2 + {\sqrt {\left( {\sqrt 3 - \sqrt 2 } \right)} ^2} = 2 + \sqrt 3 + \sqrt 2 + \sqrt 3 - \sqrt 2 = 2 + 2\sqrt 3 \\ c)\,\,\,\left( {2 + \sqrt 3 } \right)\sqrt {{{\left( {\sqrt 3 - 2} \right)}^2}} \\ = \left( {2 + \sqrt 3 } \right).\left( {2 - \sqrt 3 } \right) = 1 \end{array}

Câu 2: Giải phương trình:

\begin{array}{l}a)\,\sqrt {4x - 8} + \dfrac{1}{2}\sqrt {16x - 32} + \sqrt {9x - 18} = 21\\b)\,\,5 - \sqrt {2x + 5} = 3\end{array}

Hướng dẫn giải

\begin{array}{l}a)\,\sqrt {4x + 8} + \dfrac{1}{2}\sqrt {16x + 32} + \sqrt {9x + 18} = 21\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {DK:x + 2 \ge 0 \Leftrightarrow x \ge - 2} \right)\\\, \Leftrightarrow \sqrt {4\left( {x + 2} \right)} + \dfrac{1}{2}\sqrt {16\left( {x + 2} \right)} + \sqrt {9\left( {x + 2} \right)} = 21\\ \Leftrightarrow 2\sqrt {\left( {x + 2} \right)} + 2\sqrt {\left( {x + 2} \right)} + 3\sqrt {\left( {x + 2} \right)} = 21\\ \Leftrightarrow 7\sqrt {\left( {x + 2} \right)} = 21\\ \Leftrightarrow \sqrt {\left( {x + 2} \right)} = 3\\ \Leftrightarrow x + 2 = 9\\ \Leftrightarrow x = 7\,\left( {t/m} \right)\end{array}

Vậy phương trình có nghiêm x = 7

\begin{array}{l} b)\,\,5 - \sqrt {2x + 5} = 3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {DK:2x + 5 \ge 0 \Leftrightarrow x \ge \dfrac{{ - 5}}{2}} \right)\\ \Leftrightarrow \sqrt {2x + 5} = 2\\ \Leftrightarrow 2x + 5 = {2^2}\\ \Leftrightarrow 2x + 5 = 4\\ \Leftrightarrow 2x = - 1 \Leftrightarrow x = \frac{{ - 1}}{2}\,\left( {t/m} \right) \end{array}

Vậy phương trình có nghiệm x = - \dfrac{1}{2}

Câu 3: Cho hai biểu thức M = \dfrac{{\sqrt x }}{{\sqrt x - 2}} + \dfrac{{\sqrt x }}{{\sqrt x + 2}} - \dfrac{{x - 2\sqrt x }}{{x - 4}}và N = \dfrac{{\sqrt x + 2}}{{\sqrt x - 2}}  ( với )

a) Tính giá trị của N biết x = 16

b) Rút gọn M

c) Cho A = \frac{M}{N}. Tìm các giá trị nguyên của x để A < \dfrac{1}{2}

Hướng dẫn giải

a) Với x = 16 thì N = \dfrac{{\sqrt x + 2}}{{\sqrt x - 2}} \Rightarrow N = \dfrac{{\sqrt {16} + 2}}{{\sqrt {16} - 2}} = 3

b)

\begin{array}{l}M = \dfrac{{\sqrt x }}{{\sqrt x - 2}} + \dfrac{{\sqrt x }}{{\sqrt x + 2}} - \dfrac{{x - 2\sqrt x }}{{x - 4}}\\M = \dfrac{{\sqrt x \left( {\sqrt x + 2} \right)}}{{\sqrt x - 2}} + \dfrac{{\sqrt x \left( {\sqrt x - 2} \right)}}{{\sqrt x + 2}} - \dfrac{{x - 2\sqrt x }}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\\M = \frac{{x + 2\sqrt x + x - 2\sqrt x - x + 2\sqrt x }}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\\M = \dfrac{{x + 2\sqrt x }}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} = \dfrac{{\left( {\sqrt x + 2} \right)\sqrt x }}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} = \dfrac{{\sqrt x }}{{\left( {\sqrt x - 2} \right)}}\end{array}

c) Ta có:

\begin{array}{l} A = \dfrac{M}{N} = \dfrac{{\sqrt x }}{{\left( {\sqrt x - 2} \right)}}:\dfrac{{\sqrt x + 2}}{{\sqrt x - 2}}\\ A = \dfrac{{\sqrt x }}{{\left( {\sqrt x - 2} \right)}}.\dfrac{{\sqrt x - 2}}{{\sqrt x + 2}} = \dfrac{{\sqrt x }}{{\left( {\sqrt x + 2} \right)}} \end{array}

Để A < \dfrac{1}{2} thì

\begin{array}{l} \dfrac{{\sqrt x }}{{\left( {\sqrt x + 2} \right)}} < \dfrac{1}{2} \Leftrightarrow \dfrac{{\sqrt x }}{{\left( {\sqrt x + 2} \right)}} - \dfrac{1}{2} < 0\\ \Leftrightarrow \,\dfrac{{2\sqrt x }}{{2\left( {\sqrt x + 2} \right)}} - \dfrac{{\sqrt x + 2}}{{2\left( {\sqrt x + 2} \right)}} = \dfrac{{\sqrt x - 2}}{{2\left( {\sqrt x + 2} \right)}} < 0\\ \Leftrightarrow \sqrt x - 2 < 0\,\,\,\,\,\,\left( {2\left( {\sqrt x + 2} \right) > 0\,\forall x} \right)\\ \Leftrightarrow x < 4 \end{array}

Kết hợp với điều kiện ta được vì x nguyên nên

Câu 4: Để đo chiều rộng AB của một khúc sông mà không đo trực tiếp được, một người đi từ A đến C đo được AC = 50m và từ C nhìn thấy B với một góc nghiêng với bờ sông. Tính chiều rộng AB của khúc sông

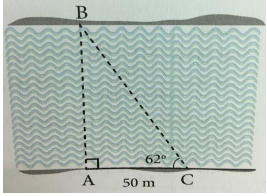
Hướng dẫn giải

Xét tam giác vuông tại A ta có:

\tan \widehat C = \dfrac{{AB}}{{AC}} \Rightarrow \tan {62^ \circ } = \dfrac{{AB}}{{50}} \Rightarrow AB = \tan {62^ \circ }.50 = 94\left( m \right)

Vậy chiều rộng AB của khúc sông là 94 m

Câu 5: Cho tam giác ABC vuông tại A có đường cao AD. Gọi AM là tia phân giác của \widehat {DAB}

a) Tính AD; AC biết DB = 18 cm; DC = 8 cm

b) Chứng minh tam giác AMC cân tại C và

c) Gọi E, F lần lượt là hình chiếu của D lên AB và AC. Chứng minh rằng {S_{AEF}} = {S_{ABC}}\left( {1 - {{\cos }^2}B} \right).{\sin ^2}C

Hướng dẫn giải

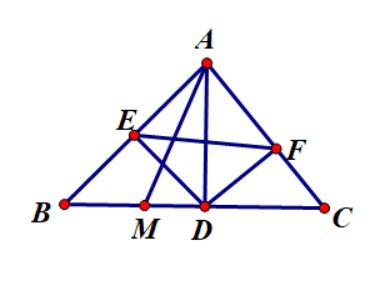
a) Áp dụng hệ thức lượng trong tam giác ABH vuông tại H ta được:

\begin{array}{l} + \,\,A{D^2} = DB.DC\\ A{H^2} = 18.8\\ A{H^2} = 144\\ AH = 12\\ + \,\,A{C^2} = A{D^2} + D{C^2}\\ A{C^2} = {12^2} + {8^2}\\ AC = 4\sqrt {13} \end{array}

b) Ta có: \left\{ \begin{array}{l} \widehat {CAM} + \widehat {BAM} = {90^ \circ }\\ \widehat {AMC} + \widehat {MAD} = {90^ \circ } \end{array} \right. \Rightarrow \widehat {DAC} = \widehat {ADC}nên tam giác ADC cân

Áp dụng tính chất tia phân giác của tam giác BAD có: \dfrac{{MD}}{{BM}} = \dfrac{{AD}}{{AB}}

Chứng minh \Delta AMC \sim \Delta BAC\left( {g.g} \right) \Rightarrow \dfrac{{AD}}{{AB}} = \dfrac{{AC}}{{BC}} \Rightarrow \dfrac{{MD}}{{BM}} = \dfrac{{AD}}{{AB}} = \dfrac{{AC}}{{BC}}

Câu 6: Cho 3 số dương x, y, z . Chứng minh rằng: \dfrac{{{x^3}}}{y} + \dfrac{{{y^3}}}{z} + \,\,\dfrac{{{z^3}}}{x} \ge x\sqrt {xz} + \,\,y\sqrt {xy} + z\sqrt {yz}

Hướng dẫn giải

Áp dụng bất đẳng thức Cô – si cho 3 số dương ta có:

\dfrac{{{x^3}}}{y} + \dfrac{{{x^3}}}{y} + \,\,{y^2} \ge 3.\sqrt[3]{{\dfrac{{{x^3}}}{y}.\dfrac{{{x^3}}}{y}.\,{y^2}}} = 3{x^2}

Tương tự ta có:

\dfrac{{{y^3}}}{z} + \dfrac{{{y^3}}}{z} + \,\,{z^2} \ge 3{y^2}

\dfrac{{{z^3}}}{x} + \dfrac{{{z^3}}}{x} + \,\,{x^2} \ge 3{z^2}

Nên \dfrac{{{x^3}}}{y} + \dfrac{{{y^3}}}{z} + \,\,\dfrac{{{z^3}}}{x} \ge {x^2} + {y^2} + {z^2}

Dễ dàng chứng minh được {x^2} + {y^2} + {z^2} \ge xy + yz + xz

{x^2} + {y^2} + {z^2} \ge \dfrac{{{x^2} + {y^2} + {z^2} + xy + yz + xz}}{2} = \dfrac{{x\left( {x + y} \right) + y\left( {y + z} \right) + z\left( {z + x} \right)}}{2}(2)

Áp dụng BĐT Cô – si ta được:

\dfrac{{x\left( {x + y} \right) + y\left( {y + z} \right) + z\left( {z + x} \right)}}{2} \ge x\sqrt {xz} + y\sqrt {yx} + z\sqrt {zy} (3)

Từ (1) (2) (3) suy ra điều phải chứng minh. Dấu “ =’’ xảy ra khi a = b = c

Tài liệu liên quan:

  • Đề thi giữa kì 1 Toán 9 - Đề số 2
  • Đề thi giữa kì 1 Toán 9 - Đề số 3

Trên đây Giaitoan.com giới thiệu tới quý thầy cô và bạn đọc tài liệu Đề kiểm tra giữa học kì 1 môn Toán 9 - Đề 4. Ngoài ra học sinh có thể tham khảo thêm một số tài liệu liên quan: Lý thuyết Toán 9, Luyện tập Toán 9, Giải Toán 9 Tập 1, ....

  • 584 lượt xem
Chia sẻ bởi: Lê Thị Thùy
Tìm thêm: Toán 9 Đề thi học kì lớp 9
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Chủ đề liên quan